Блок 9 производит расчет входных сигналов звеньев СЭП X [I] h соответствии с уравнениями связи, вид которых определяется структурой исследуемой системы.

Блок 10 выполняет вычисление выходного сигнала /-го звена СЭП Y [/], используя подпрограмму универсального звена.

Блок обеспечивает переход к (/ + 1)-му звену структурной схемы.

Блок ]2 осуществляет контроль выполнения условия того, что рассчитаны выходные сигналы для всех К звеньев СЭП.

Блоки 13-17 обеспечивают переход к следующему, {J -\- 1)-му, циклу расчета, если используется численный метод первого порядка, или ко второй итерации на У-м цикле расчета, если используется численный метод второго порядка.

Блок 18 служит для контроля конца вычисления при заданном времени Тк- Если длительность исследуемого процесса заранее неизвестна, то блок 18 исключается и программа оказывается зацикленной (штриховая линия).

Таблица bi

PflJ

Нелинейное или Зремвнное звено

05о5ш,елная однозначная нелинейность

Структурная схема алгоритма

v---iAz[i]! тнхил

Q-Stan Mill

5 I Нет

lot"-"00"

Z. -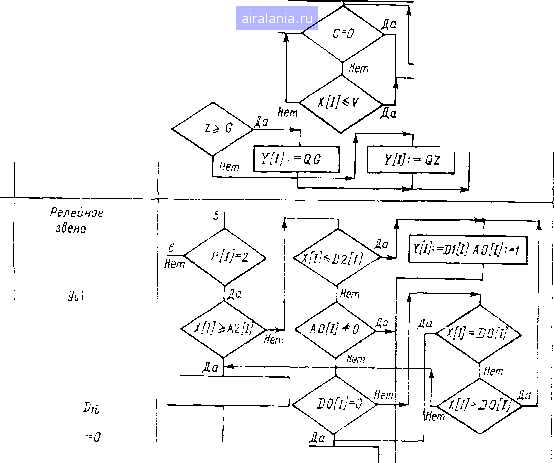

i e/

F==DOll] S=31[I]

BQ[I]X[I]

Продолжение табл. 1-1

при Vqi=0

fSOHmoBaHue no уродню

Запаздывание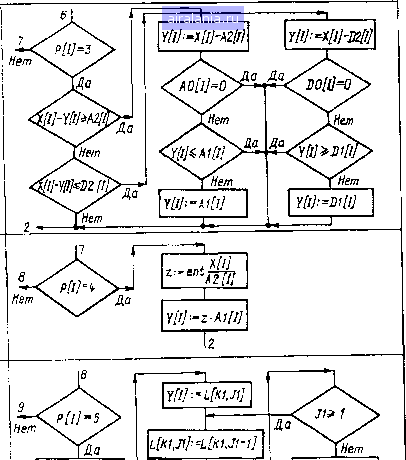

0 4 ь Ац-номер строки;

К1--А1[1]

J1:=J1-1

JV = 0

-Vz-

Конец вычисления определяется оператором на основании результатов р/ичета.

Цифровое моделирование позволяет просто построить анализатор ка-чсгтиенных показателей переходного процесса: максимального динамиче-1 и<1го отклонения регулируемой координаты, времени переходного процесса, инимральных оценок, информацию о которых можно использовать при оп-шмизации СЗП.

Рассмотрим подробнее модель универсального звена, которая состоит и1 линейной части, описываемой передаточной функцией

xcip) aip-\-аир-V a-ii

м 1!е.11инейной части.

Структурная модель линейного динамического звена с передаточной функцией (1.68) представлена на рис. 1.11,6. Однако часто моделируемые <пМI имеют динамические звенья первого порядка, поэтому использование юлько математической модели звена второго порядка будет создавать зна-чшельную избыточность программы. Введем три вида линейных звеньев: niitioro, первого и нулевого порядка. Структурная модель звена первого im)Muu<a изображена на рис. 1.11, е.

wap)-

Продолжение табл. 1-1

Табличная нелинейность

aoi = b степень полинома a, = max si

Аналитическая нелинейность

Оц - номер формулы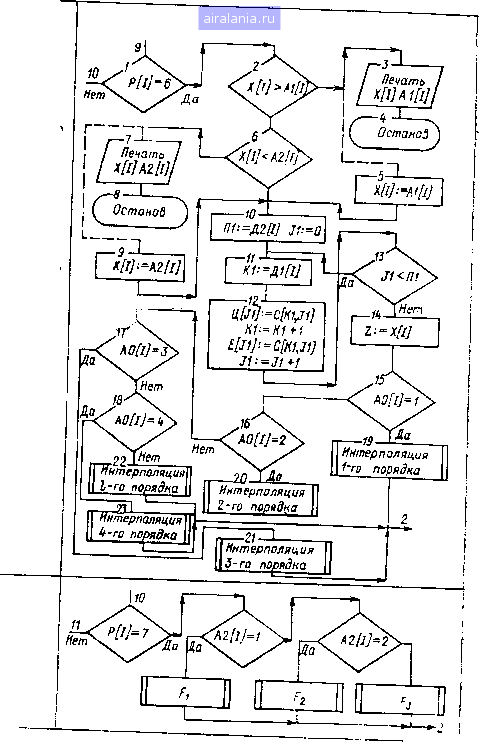

Структурная схема алгоритма моделирования линейного звена при использовании методов численного интегрирования Эйлера и Эйлера-Коши показана на рис. 1.12. Метод интегрирования задается посредство?л идентификатора Ш У ]• при Ш [1] = \ - метод Эйлера, при Ш [1] = 2 - метод Эйлера-Коши. Непосредственно алгоритм моделирования линейного звена включает в себя блоки с по 22; другие блоки, показанные на рис. 1.12, служат для пояснения алгоритма. На рис. 1.12 использованы следующие обозначения; Т - текущее время; Ш [О) - шаг интегрирования; Ш [2] - 42

Идштификатор номера итерации: для метода Эйлера Ш [2] = О, для метода РЙлера-Коши Д/ [2] = О на первом шаге итерации и Д/ [2] = 1 на втором Миге; J - счетчик номера звена структурной схемы; X [I] ~ входной сиг-Иял /-го звена; Р [I] - идентификатор типа звена; Р [/] = О -линейное iBiiio; Р [/] = 1 - обобщенное однозначное нелинейное звено; Р [I] - 2 ~ млеГиюе звено; Р [/] == 3 - люфт; Р [/] = 4 ~ квантование по уровню; Р [/ = 5 - «чистое» запаздывание; Р [/] = 6 - нелинейное звено, за-Йёиаемое таблично; Р [/] = 7 - нелинейное звено, задаваемое в аналити-NiCKOM виде; К1, Л, П1 - идентификаторы индексов и целочисленных переменных; / - счетчик циклов расчета; П - шаг печати.

Для хранения переменных вида 5 [/С/, /], R [К1, 1], X [К1, /] выделяются двухмерные массивы, имеющие по две строки. Если численное пи-Мгрирование производится по методу Эйлера, то указанные переменные могут описываться одномерными массивами. При использовании численного )квп)да Эйлера {Ш [1] = I, Ш [2] - 0) вычислительный процесс расчета выходного сигнала 1-го линейного звена организуется в соответствии с бло-ИАМи 1-6, 10, и, 14-21 структурной схемы алгоритма (рис. 1.12). После нычисления Y [1] происходит переход к расчету выходного сигнала (/ Н- ])-го риена и т. д. до К-го звена, затем содержимое счетчика циклов J увеличи-ввется на единицу и управление передается блоку / и т. д.

* Если используется метод Эйлера-Коши (идентификатор Ш [1] ~ 2), I мымислительный процесс организуется иначе. На первом шаге вычисления i мы ход ные сигналы интеграторов определяются в соответствии с формулами

* блоков 14, 15 (т. е. по методу Эйлера), при этом используются блоки 1-5, /*, 8, 10-21 структурной схемы алгоритма. После вычисления выходных сигналов для всех К звеньев системы идентификатор Ш [2] принимает еди-liiiiHoe значение (блоки 26, 27, 30) и производятся вычисления на втором !Ийге итерации в соответствии с блоками 2-5, 7, 9-12, 16-23 (состояние «ч«?тчика циклов J не изменяется).

I Выходные сигналы интеграторов вычисляются по методу Эйлера-Коши

спгласно формулам, записанным в блоках 22, 23.

После вычисления выходных сигналов всех К звеньев СЭП происходит переход к следующему циклу расчета (блоки 25-29, 1 и т. д.).

Структурные схемы алгоритмов моделирования нелинейных и временных звеньев приведены в табл. 1.1.

Для обозначения параметров нелинейных и временных звеньев используются идентификаторы линейного звена, С помощью алгоритма обобщенного однозначного нелинейного звена можно моделировать нелинейные зависимости во всех четырех квадрантах посредством присвоения параметру Q значении sign All или signDji.

Для реализации «чистого» запаздывания организуется массив L, имеющий длину x/At. Номер строки массива определяется значением коэффициента Л1 [I] = О, \, 2, . . . , N. Если время запаздывания т велико, а шаг интегрирования мал, то целесообразно использовать другие способы реализации запаздывания [52].

Для хранения табличных нелинейностей выделяется двухмерный мас-СИ1) С. Коэффициенты нелинейного звена обозначают следующие параметры: Л2 [/]-число точек нелинейной характеристики Nj; Д1 [/] - номер строки / массива С, где хранится аргумент нелинейной функции; значения функции заносятся в (/ -f 1)-ю строку массива С; АО [/] -степень поли-тмл Лагранжа, используемого для интерполяции нелинейной функции мржду узлами; А1 [/], А2 [I] - максимальное и минимальное значения г1р1умента; Ц [Л] и Е [Л] -одномерные массивы.

Подпрограмма данного нелинейного звена предусматривает использова-име интерполирующих полиномов Лагранжа до четвертого порядка, что *1хнптывает практически все виды нелинейностей, встречающиеся в систе-мпх электропривода.

Аналогично можно построить алгоритмы с использованием других способов интерполяции.

Контроль нахождения аргумента нелинейной функции xi в диапазон, допустимых значений производится блоками 2 и 6.

В зависимости от конкретного вида нелинейной функции при выход*, аргумента xi за допустимый диапазон может быть предусмотрено продолжение (в табл. 1.1 этот путь показан штриховой линией) или прекраш,ение вычислений (блоки 3, 4 и 7, 8).

Пример. Рассмотрим использование программы цифрового моделирования на примере СЭП, структурная модель которой показана иа рис. 1.13. Все звенья системы нумеруются начиная с нуля-

Система регулирования состоит из регулятора скорости PC с блоко.м ограничения (звенья О и /), тиристорного преобразователя ТП (звенья 2 и 3), двигателя постоянного тока (звенья 4, 5, 6), задержанной обратной связи по току (звено 7) и главной обратной связи по скорости (звено 8).

В[0] из

PC (D

doCOSjj-Uy Um

я.ДСП

В[2] Мс

Ш[9]

Нч Л"

Рис. 1.13. Структурная схема нелинейной СЭП

Исследуемая СЭП является нелинейной за счет ограничения выходного сигнала регулятора скорости значением L/p. с, о (звено 1, имеющее нелинейную характеристику вида HI); наличия зоны нечувствительности в цепи обратной связи по току, учитывающей также ограничение выходного сигнала датчика тока максимально допустимым значением f/дтах (звено 7 с нелинейностью вида Н2); нелинейности НЗ, обусловленной невозможностью реверса тока якоря двигателя, так как рассматривается нереверсивный электропривод, и ограничением допустимого значения тока двигателя /я. доп (звено 5); нелинейности регулировочной характеристики тиристорного преобразователя, задаваемой аналитически или таблично (звено 3). В данном случае она задается аналитически.

Подпрограмма расчета входных сигналов звеньев, составляемая на основании структурной модели системы, имеет следующий вид:

лгц = 5о - Уб\ = г/4;

1 = Уо; = Уь - кВг;

Xz - Ух- ko. -vyv X-j = д. Уо

Xiys kcBi - yjkj,

*i Ад. Tl o. T - соответственно коэффициенты передачи датчика тока и об-JlTHoii связи по току; - коэффициент передачи двигателя по управляю-Щму воздействию; - коэффициент передачи ТП по возмущению AUc-Исходные данные для расчета сведены в табл. 1.2. В табл. 1.2 приняты следующие обозначения для параметров исследуе-Мвй системы электропривода: х, т, Тр - постоянные времени ПИД-регу-йЯТОра скорости; k, Г,., п - соответственно коэффициент передачи и постоян-Мйя времени тиристорного преобразователя; /?я. ц - сопротивление якорной Цепи привода; Тя, Тэм - электромагнитная и электромеханическая посто-йпиые времени привода; ко. с, То. с - соответственно коэффициент передачи Н постоянная времени обратной связи по скорости; £0. - максимальнее значение выпрямленное ЭДС и максимальное значение сигнала управ-Лшия ТП.

Подпрограмма аналитической нелинейности (звено 3) записывается так:

~ А cos {тех il А oi). (1.69)

После выполнения всех подготовительных операций переходят к решению задачи, выбирая метод численного интегрирования, шаг интегрирования, шаг печати и задавая входные воздействия в соответствии с программой исследования.

Таблица 1.2

1 5 РАСЧЕТНО-ЭКСПЕРИМЕНТАПЬНЫЕ МЕТОДЫ " ИССЛЕДОВАНИЯ СИСТЕМ ЭЛЕКТРОПРИВОДА

При исследовании динамики систем электропривода ".ТпялТхПриличные ctdvktvd ные методы, описанные в предыдущих параграфах. При моиениекоТреТого метода или комбинации методов зависит от поставлен-