ных задач, сложности системы и этапа исследования. Рациональный выбор методов позволяет с наименьшими затратами времени провести возможно более полный анализ работы СЭП. Вместе с тем использование только рас-четно-теоретических методов не всегда оказывается эффективным при исследовании сложных СЭП. Такие системы имеют высокий порядок, что затрудняет нахождение полюсов и нулей передаточных функций; параметры объекта оказываются взаимосвязанными, а это, в свою очередь, затрудняет выделение существенных параметров. Кроме того, реальная многомассовость механической системы и наличие нелилейных упругих связей первого и второго рода значительно осложняет разработку адекватных моделей и расчет необходимых параметров.

В этих условиях целесообразно применять расчетно-экспериментальные методы, т. е. методы, сочетающие теоретические расчеты и экспериментальные исследования СЭП на физических макетах или действующих объектах. Это позволяет выделить сущестнемпые параметры и связи системы, определить трудно рассчитываемые механико-технологические параметры объекта и в конечном итоге идентифицировать математическую модель реальной системы. При расчете взаимоснязанкых СЭП нередко оказывается эффективным чередование расчетных и экспериментальных методов на каждом конкретном этапе исследования, начиная с разрабоки адекватной модели объекта и кончая синтезом структуры и параметров регуляторов.

С этих позиций рассмотрим применение расчетно-экспериментальных методов для идентификации динамических параметров унифицированных систем подчиненного регулирования.

Идентификация динамических параметров и структуры объектов регу лирования. Методы экспериментального определения параметров ЭП рассмотрены в ряде работ [13, 14, 15, 63], Эти методы применимы к исследованию линейных и нелинейных систем, хотя некоторые из них базируются на использовании специальной аппаратуры. Поэтому большое значение приобретают способы определения динамических параметров, использующие стандартную аппаратуру \\ позволяющие с необходимой точностью определить искомые параметры. Эги способы изложены ниже применительно к разработанному математическому описанию, что позволяет реализовать теоретические рекомендации по оптимизации динамики в практике наладки промышленных СЭП,

Определение механических постоянных времени объектов. Механическая постоянная времени однодвигательного ЭП Ts = 7м. д + Тм определяется по формуле

(1.70)

где /2*!= "д + .м - суммарный приведенный момент инерции привода. Физически есть время, в течение которого привод разгоняется в режиме холостого хода (М = 0) от О до О). с при /я = /я. с или при динамическом токе, равном /я. С) когда Мс ф 0. Если при этом Мс не зависит от скорости ЭП, что с известной степенью приближения справедливо для ряда промышленных ЭП, то эксперимент по определению в системах подчиненного регулирования вьшолняется следующим образом. Привод разгоняется до базовой скорости ©с в режиме ограничения регулятора скорости («под отсечку») при пусковом токе /a.o=const (рис. 1.14). При этом определяется время пуска t, что может быть сделано по тахограмме или по секундомеру с помощью амперметра в якорной цепи двигателя. Тогда искомое значение Гми определяется формулой

r„s = ink, (1.71)

где k - (/я. о - я.с)/я. с - кратность пускового тока.

Механическая постоянная времени двигателя Т.д при выбранном базовом режиме находится по формуле

Физически Гм.д есть время, в течение которого электродвигатель разго-ЙШТСЯ в режиме холостого хода (Мс = 0) от О до «д. при /я = /я. с- Для щепериментального определения Г.д следует осуществить пуск двигателя, феоеди не иного от механизма, при токе якоря /я = я. с + я.х. где /я.х - fOH холостого хода двигателя. При этом по тахограмме Од.с(0 измеряется

Цтя пуска, равное Г, д.

Если /я.х С /я. с. то пуск двигателя может быть произведен при токе §Граничения /я. о. выбранном в предыдущем опыте по определению ГмБ-Рри этом фиксируется время пуска двигателя /„.д- Постоянная времени Гм. д Шределяется формулой

T. = tn.p,k, (1.73)

где k - кратность пускового тока, определяемая из формулы (1.71). По-fitOHHHafl времени механизма находится по выражению

Гм-Г„2-Гм.д. (1.74)

Рассмотрим особенности определения механических постоянных вре-мгии в многодвигательных СЭП. В механизмах с прижимом рабочих валов (прессовые секции бумагоделательных М<1шин, клети прокатных станов и др.) i все моменты инерции и сопротивления я.о дпкгателей н механизма приводятся к одному валу [59]. При этом мехакиче-гкая постоянная времени привода определяется формулой

7м2 = 2С0сШс, (1.75) 4,

1Д0 «с - скорость вала, к которому Приведены и Мс;

1=1 1=1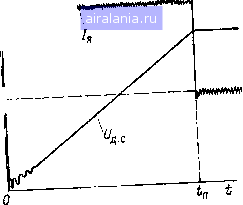

1=1

Рис. 1.14. К определению механических постоянных времени " электропривода

- соответственно моменты инерции двигателей и механизма

и моменты сопротивления рабочих валов. Физически jTjjs - время пуска «-двигательного привода на скорость сос при динамическом токе /я.с = п

/я. ci» где /я. ci -токи двигателей в статике. В соответствии с этим экспериментальное определение сводится к разгону ЭП на заданную ско-

рость при токе ограничения/я. о = /я.ор где /«. ot- пусковые токи дви-гателей. При этом регистрируется время пуска Искомое значение Гм2

определяется по формуле (1.71)

В многодвигательных СЭП с разомкнутыми или замкнутыми упругими гнязями второго рода (бумажное полотно, металлическая полоса, технические сукна, синтетические сетки и т. п.) все моменты инерции и сопротивле-1тя двигателей и рабочих органов приводятся к выбранным валам «своих» секций, например к валам двигателей при скорости ленточного материала Ус-

При этом механические постоянные времени отдельных приводов будут

TM2i = Jzici/Mci, (1-76)

где (Oct - скорости валов, к которым приведены Jz,i и Mci\ J2i~ fii +«N1

Mci - моменты сопротивления рабочих валов секций.

Физически Ti - время пуска i-ro привода на скорость (ni при динамическом токе, равном /я.с/- В соответствии с этим экспериментальное определение Tmsj сводится к разгону г-го привода под током /д oi на заданную скорость tOcti соответствующую скорости движения материала сс, при отсутствии упругой связи второго рода (в системах с замкнутыми упругими связями последние предварительно снимаются). При этом фиксируется время пуска каждого привода tni-. Искомые значения Tsi будут

TuHi-tiki, (1.77)

где ki = (/я. Of - /я. ы)/я. ci

Механические постоянные времени двигателей Т.дв многодвигательных ЭП как при прижиме рабочих валов, так и при наличии секций с упругими связями второго рода определяются посредством пуска двигателей, отсоединенных от механизма, на заданную скорость. Методика идентификации Тм. д1 аналогична таковой для однодвигательных приводов. В частности, при /я. х( С-я. Ci разгои i-ro двигателя осуществляется подтоком я.ог» и при этом фиксируется время пуска п.д1- Постоянные времени Гмд! находятся по формуле

Тм. Д1 п.д£ь (1-78)

где ki - кратность пускового тока двигателей, определяемая из выражения (1.77).

Постоянные времени механизма при прижиме валов или при наличии упругих связей второго рода рассчитываются по формулам:

Ты Т: - 2 м. = MSt - м. дг> (1 -79; 1.80)

Найденные значения мехагических постоянных времени могут быть введены в дальнейшие расчеты непосредственно 1гли использованы для определения первичцых параметров привода, и частности моментов инерции звеньев механической системы.

Идентифитцич объектов с упругими связями. При исследовании динамики СЭП с упругими связями необходимо знать структуру объекта и параметры упругих связей. Определение структуры и параметров расчетным путем нередко вызывает значительные трудности, так как реальные механические системы чаще всего являются многомассовыми, с распределенными параметрами, а значение и характер диссипативных сил заранее неизвестны. Поэтому возникает задача разработки рациональных расчетно-эксперимен-тальных методов идентификации систем с упругими связями.

При экспериментальном исследовании механических систем нередко удается определить существенные частоты упругих колебаний, что дает воз-.можность эквивалентировать многомассопые механические системы более простыми, например двух- или трехмассовыми, системами. При этом структура математической .модели объекта упрощается и становится удобной для анализа. В работе [13 J описаны интересные исследования, выполненные с помощью экспериментальных логарифмических частотных характеристик и поз водившие идентифицировать весьма сложный многомассовый объект управления радиотелескопа. Подобные исследования применительно к переходным характеристикам были проведены для секций бумагоделательных машин [59]. Они, в частности, позволили эквивалентировать многомассовые механические системы секционных приводов двухмассовыми системами.

Весьма важны.м является получение исходной информации о параметрах упругих колебаний и связи этой информации с параметрами идентифицируемой математической модели механической системы. При возможности проведения активного эксперимента необходимо создать тем или иным способом переходный процесс в системе двигатель-механизм, вызвав упругие колебания. Наиболее простым и удобным в производственных условиях способом является подача ступенчатого управляющего воздействия, направленного на увеличение скорости ЭП н при котором регулятор скорости входит

I режим ограничения выходного напряжения (t/p.c - fp. со)» а ток якоря Дшигателя достигает значения /д = /я. о- При этом регистрируется изменение напряжения датчика скорости двигателя /д.с(0 Р- - о пред-тавлена осциллограмма д. с (О в системе с упругостью первого рода, а на рис. 1.15, б - в системе с упругими связями первого и второго рода. На обеих осциллограммах четко видны упругие колебания якоря двигателя, и.меющие атухающий характер; причем на осциллограмме (рис. 1.15, б) упругие колебания первого рода наложены на колебания второго рода. Естественно, I последнем случае скачок тока якоря двигателя должен быть выбран таким, чтобы не нарушить нормальное течение технологического процесса.

Следует заметить, что переходная характеристика t/д. с (О иа рис. 1.15,й является начальной частью осциллограммы U„.c{t), показанной на рис. 1.!4.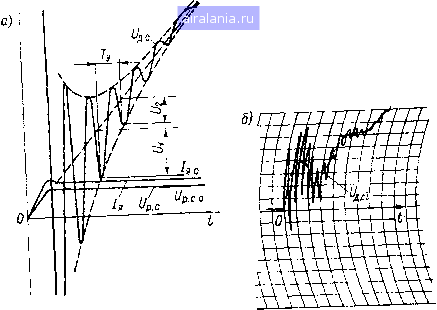

Рис. 1.15. К определению параметров упругих колебании первого и второго рода

Поэтому эксперимент по определению механических постоянных времени пр1[вода и параметров упругих колебаний механической системы является единым, что позволяет унифицировать проводимые исследования реальных объектов.

Рассмотрим вначале систему с упругостью первого рода. Поскольку упругие колебания д. с(0 затухают приблизительно по экспоненциальному закону (см. рис. 1.15, а), то это дает возможность эквивалентировать реальную механическую систему двухмассовой системой с определяющим влиянием сил линейно-вязкого трения [37]. Для определения частоты о)у и постоянной йремени затухания Ту свободных колебаний двухмассовой упругой системы следует взять участок осциллограммы L/д, с (0> котором ток якоря /я = /я. о- Постоянство /я при колебаниях t/д. с объясняется слабостью внутренней обратной связи по ЭДС двигателя при быстродействующем контуре тока якоря. Тогда Шу и Ту могут быть определены по формулам:

соу"" • -----. (1.81)

In {UilUz)

Теперь необходимо связать «-йденные значения о, .у с математической модели объекта, изображенной на рис. 1.0, перед

функция между относительными изменениями момента и скорости двигателя, полученная по приведенной структуре, может быть представлена в виде

HiP) T,,P{qVP+TaP + l)

(1.82)

где r„s = м.д+ Гм; q - Гм.д/П,.

Выражение Л„ „ ~--~ - можно записать, в следующей форме:

qTTp+TdP ! 1

ту -1- 21Т.р + 1

Гу, (р)

7]уг21Г1Р + 1

(1.83)

С2 -

2 л/ТмГс

Характеристическое уравнение выражения (1.83), определяющее сво бодное движение упругой системы, будет

714-21175+1=0.

Корни последнего уравнения находят по формуле

Pi, 2 -~= -

(1.84)

(1.85)

Поскольку i<l, то корни выражения (1.85) будут комплексными:

Рь 2= - С2у ±/а)у, (1.86)

Отсюда

vl + (С0уТу)2

vl + (t0yTy)3

(1.87)

Последние выражения связывают параметры математической модели с параметрами упругих колебаний, определенными по формулам (1.81), Следует заметить, что в сильноколебательной системе (где 0,1) формулы (1.87) могут быть упрощены:

Ti - ; (1,88)

0)уТу

Определим обобщенные параметры ?с и Td упругой связи первого рода через известные величины, найденные как расчетным, так и экспериментальным путем. Из уравнений (1,8?) и (1.83) следует

Тг =

; 7 = 2111.

(1.89)

Подставляя в последние формулы значения Т и li из (1.87) или (1,88), Получим

Тс =

«ли

Л[1-{«уТу)2

Td =

1 4 (<0уту)2

ШуТу

(1.90)

(1.91)

Таким образом, определив экспериментально параметры (Оу и Ту сво-<5одных колебаний упругой системы, можно найти по приведеннымвыше формулам необходимые для расчета динамические параметры математической модели.

Полезно также получить формулы, непосредственно связывающие параметры (йу и Ту упругих колебаний с параметрами механической системы. Из формул (1.90) и (1.91) следует

29ГмТс Та

Ту =

(1.92) (1.93)

Выражая постоянные времени через первичные параметры механической системы, окончательно имеем

юу ---

2qJ„

Ту--;- ,

(1.94)

(1.95)

где с, b - приведенные коэффициенты жесткости и вязкости механической передачи; q = д/(д + м)-

Обратимся к общему виду механической системы с упругими связями лервого и второго рода. Как отмечено в § 1.2, упругие связи второго рода могут быть разомкнутыми (бумажное полотно, металлическая полоса и т. п.) II замкнутыми (общая «одежда» секционных ЭП бумагоделательных машин). Обычно частота упругих колебаний второго рода существенно меньше частоты колебаний первого рода, так что упругие колебания первого рода оказываются наложенными на колебания второго рода, как это показано на рис. 1.15, б. В этом отношении осциллограмма t/д. ct (О идентична в системах с разомкнутыми и замкнутыми упругими связями второго рода, а затухание колебаний имеет практически экспоненциальный характер.

Рассмотрим сперва систему с разомкнутыми упругими связями при ра-неистве параметров смежных ветвей ленты, что справедливо в первом приближении. Передаточная функция между моментом и скоростью двигателя может быть представлена в виде (см. § 2.3)

W, (р) -

Уд(р) ГмУ" + Гр + 1

."д (Р)

qTuTcP + TdP + 1 ГбР1

"v 2Мф

2kvk

(1,96)