тимальными как по управлению, так и по возмущению при малой чувствительности к вариации параметров объекта. С этой целью проведем синтез параллельной коррекции контура, настроенного на СО, когда в объекте регулирования имеется звено \!{Tqp). Охватим объект регулирования корректирующим звеном с передаточной функцией (р) (см. рис. 2.1, а) и потребуем, чтобы передаточная функция типового разомкнутого контура (р) с учетом этого звена и настройки регулятора на СО соответствовала настройке на ОМ, т. е. выражению (2.3). Тогда требуемая передаточная функция корректирующего звена будет

W(p).JAZiP±IL, (2.11)

Передаточная функция замкнутого контура по возмущению теперь станет

WAp)-~=----"Щ- . (2Л2)

Г) {2Т%р + 2Тр.-г~\

Соответствующие ЛАХ W, и W, построенные по выражениям (2.3), (2.11) и (2.12), представлены на рис. 2.2. Анализируя характеристику W, можно заметить, что длительность переходного процесса при возмущении не зависит от Tq и определяется величиной Ts, а максимальное динамическое отклонение регулируемой величины меньше, чем при настройке контура на СО.

Рассмотрим динамику контура при изменении параметров объекта k, Т. Обозначим уТ, = ak, = = -TjH, где Гон, и Гн - номинальные (начальные) значения То, и Т, при которых рассчитываются параметры регулятора и корректирующего звена. Давая последовательно приращение каждому из указанных параметров объекта, можно записать передаточные функции разомкнутого контура в виде

(р) - 77.-; (2.13)

где Wn{p)

ТР (Р) =

Тр V 1

(>Т2нР+ 1)4Г2нР TshP -t-1

(2.14)

(2.15)

TzPiTp+l)

При Y О или а со передаточная функция (р) = Wu (р). Соответствующая ЛАХ показана на рис. 2.2 штрихпунктирной линией. Из анализа характеристики следует, что при уменьшении

То или увеличении быстродействие и устойчивость контура возрастают, причем при То О или k- оо контур становится инвариантным к их изменению, имея частоту среза ©с == 2/Т.

При увеличении То или уменьшении быстродействие и устойчивость контура снижаются (см. ЛАХ Wp, показанную на рис. 2.2 двойной штрихпунктирной линией), однако и в рассматриваемом случае включение параллельной коррекции обеспечивает меньшую чувствительность динамики контура к изменению указанных параметров. Это объясняется большей устойчивостью скорректированного контура, имеющего при этом ЛАХ типа -1, -2, -1, -2, по сравнению с контуром, имеющим ЛАХ типа -2, -1, -2 и настроенным на СО.

При О выражение (2.8) станет

что обеспечивает ЛАХ контура [без (р)] типа -2, -1 при частоте среза со. = 1/(2Т2). При введении коррекции из выражения (2.15) следует

WAp)--iIsHP± i- 2.17)

Соответствующая ЛАХ ttp показана на рис. 2.2 пунктирной линией (точками), откуда видно, что при снижении Т устойчивость контура возрастает. При увеличении Т устойчивость контура в обоих случаях снижается, однако чувствительность контурна с коррекцией будет существенно ниже вследствие его большей устойчивости в номинальном режиме.

Исследования динамики контура машинными методами (на АВМ и ЦВМ) полностью подтвердили выводы, полученные при анализе частотным методом. На рис. 2.3 представлены нормированные переходные характеристики контура при ступенчатых управляющем и возмущающем воздействиях до (штриховые кривые) и после (сплошные кривые) введения параллельной коррекции. После введения Wk (р) переходная функция контура по управлению полностью соответствует настройке на ОМ. Следует заметить, что при настройке контура на СО и включении на его вход апериодического фильтра с постоянной времени Тф = АТ соответствующий переходный процесс имеет вид, показанный на рис. 2.3 штрихпунктирной линией. При этом время регулирования возрастает приблизительно в 2,3 раза. Динамическая ошибка по возмущению снижается после введения коррекции на 22% при практически одинаковом с настройкой на СО времени переходного процесса. Из рис. 2.3 также видно существенное снижение чувствительности контура к изменению параметров объекта, в частности к изменению То.

Анализируя полученные результаты, можно сделать вывод, что настройку регулятора и параллельного корректирующего звена в условиях широкого изменения параметров объекта (То, k, Т)

целесообразно выполнять при максимальном значении Tq, и минимальном значении k.

Рассмотрим теперь реальный контур системы подчиненного регулирования, структурная схема которого показана на рис. 2.1, б. На схеме введены дополнительные обозначения: пж - коэффициент настройки и малая постоянная времени внутреннего контура (например, контура тока), Гд-постоянная времени датчика обратной связи внешнего контура {контура скорости). Как и ранее, параметры ПИ-регулятора выбираются по условиям (2.6), а параметры параллельной коррекции - по формуле (2.11), где = = Гд + щТ.

При условиях Tvp -\- 1 « (ГдР + 1) {nj-p + 1); щТр- +

+ iflTnP + 1 пТр -- 1 и » передаточная функция разомкнутого контура будет

(Р)

При отсутствии Wk(p) соответственно имеем

(р) =

4TSP+1

(2.18)

(2.19)

ЬТ\р[Тр-\)[п,Туп,Тр+\)

Анализ выражений (2.18) и (2.19) показывает, что и в рассматриваемом случае введение (р) обеспечивает перевод настройки контура из СО в ОМ со всеми указанными выше преимуществами предложенного способа коррекции.

При практической реализации корректирующего звена следует учитывать режим работы контура «в большом», когда регулируемая координата у изменяется в широких пределах. Во избежание насыщения регулятора в стационарном режиме и нарушения функционирования системы токоограничения корректирующая связь должна быть гибкой. При этом коррекция реализуется как пропорционально-дифференциальное звено с передаточной функцией

ЬТ,Тр{ТрА-\)

(Р) =

22 72 (lOrsP+OCO.lTsP 4-1)

(2.20)

что обеспечивает характеристики звена в зоне существенных частот, близкие к требуемым по условию (2.11). Коррекция реализуется с помощью операционных усилителей по схеме, представленной в нижней части рис. 2.3 (схема б). При значительном влиянии высокочастотных пульсаций передаточная функция коррекции может быть выбрана в виде

ЧТО дает более грубое приближение к требуемым характеристикам звена. Соответствующая электрическая схема звена показана там же (схема а).

На основании проведенного анализа можно сделать следующие выводы:

а) введение в унифицированный контур АСР синтезированного выше параллельного корректирующего звена позволяет получить оптимальные динамические характеристики контура по управлению и возмущению и существенно снизить его чувствительность к вариации параметров объекта регулирования;

б) применение предложенного способа коррекции целесообразно в унифицированных электроприводах с широким изменением параметров объекта, когда от АСР требуются максимальное быстродействие и высокая стабильность работы при внешних и внутренних (параметрических) возмущениях.

2.2. ОПТИМИЗАЦИЯ ДИНАМИКИ УНИФИЦИРОВАННЫХ СИСТЕМ ЭЛЕКТРОПРИВОДА С УПРУГИМИ СВЯЗЯМИ ПЕРВОГО РОДА

Экспериментальные исследования систем электропривода ряда промышленных агрегатов показывают существенное влияние упругости механических передач на динамику СЭП. Такое влияние приводит к появлению незатухающих колебаний в СЭП, перенапряжениям и ударам в механических связях, повышенному искрению на коллекторах электрических машин, а в наиболее тяжелых случаях- к нарушению технологического процесса и выходу из строя механического оборудования. Все это требует принятия необходимых мер при оптимизации систем регулирования и разработки соответствующих корректирующих устройств.

Рассмотрим оптимизацию линеаризованных унифицированных вентильных СЭП постоянного тока. При математическом описании СЭП удобно воспользоваться полученными выше НСС механической части ЭП с соответствующим добавлением регулирующей части. Учитывая возможности эквивалентирования многомассовых механических систем, ограничимся рассмотрением двухмассовых систем. Вместе с тем такое упрощение оказывается приемлемым для многих промышленных СЭП. Опытные виброграммы свободных упругих колебаний секций агрегатов целлюлозно-бумажной, металлургической и других отраслей промышленности соответствуют двухмассовым системам с определяющим влиянием сил линейно-вязкого трения [25, 56, 59].

На рис. 2.4, а представлена НСС системы электропривода, оснащенной унифицированной АСР скорости с подчиненным контуром тока якоря двигателя. Силовая часть ЭП соответствует рис. 1.5, б, остальные обозначения следующие: В7р. (р) - передаточная функция регулятора скорости; Р2. - динамический коэффициент усиления и постоянная времени ПИ-регулятора тока якоря; kn, Т. ц-нормированный коэффициент передачи и постоянная времени тиристорного преобразователя (ТП), причем /гп = т.пз.с.с/т.п.с; т.п - коэффициент передачи ТП; (Уз.е. с» т. п. с - напряжение задания

скорости ЭП и ЭДС тиристорного преобразователя в статике; k, Тд. я - нормированный коэффициент передачи и постоянная вре-

мени датчика тока якоря (ДЯ), причем = д. яя-с/з.с. с? йд.я - коэффициент передачи ДЯ; /я.с-ток якоря двигателя в статике; Тд.<; - постоянная времени фильтра датчика скорости;

3. с ~ 3. сз. с. с! >р. с ~ р. с3. с. с5 я ~ р. яз. с с! *Д. я ~

~ д. яз. с. с> Jfl. с ~ л. сз. сс-

При анализе данной структуры в первую очередь необходимо оценить влияние внутренней обратной связи по ЭДС двигателя, показанной на рис. 2.4, а штриховой линией, и возможности пренебрежения ею.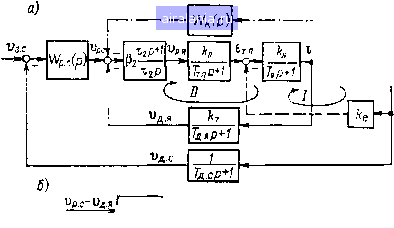

Kz(p)

Рис. 2.4. Нормированные структурные схемы СЭП с упругой связью первого

рода

Влияние внутренней обратной связи по ЭДС двигателя на динамику системы. Влияние внутренней обратной связи по ЭДС двигателя на динамику жесткой, т. е. одномассовой, системы регулирования скорости с подчиненным токовым контуром исследовано в ряде работ [49, 58 J. Это влияние приводит к статизму токового контура при предельном токоограничении и к увеличению перерегулирования тока якоря в переходном процессе. Влияние обратной связи по ЭДС двигателя существенно при относительно малых значениях электромеханической постоянной времени привода Ty, и снижается по мере роста T,, по сравнению с суммарной малой постоянной времени токового контура Тг.

Установим, при каких условиях возможно пренебрежение обратной связью по ЭДС двигателя в системе с упругой механической передачей и каков характер влияния этой связи на динамику СЭП. Из структурной схемы (рис. 2.4, а) видно, что влияние обратной связи по ЭДС двигателя сказывается в первую очередь на динамике токового контура. Передаточная функция разомкнутого

токового контура с учетом обратной связи по ЭДС двигателя, со-<:тавленная с помощью правила Мэзона непосредственно по структурной схеме (рис. 2.4, а), может быть записана в виде

1 ч-

kkeiT,TcP" + TdP+l) Тир {Т,р -f 1) {qTT,p Тар + 1) J

(2.22)

где Гр2 (р) = /[поТгР {ТР + 1) ] - передаточная функция разомкнутого токового контура без учета обратной связи по ЭДС двигателя; Тз = Тт.п + Тд, я\ «о - коэффициент настройки (при По 2 контур настроен на оптимум по модулю); <7 = Т.д/Т.,;

На основании выражения (2.22) на рис. 2.4, б построена НСС токового контура, позволяющая наиболее просто исследовать влияние обратной связи по ЭДС двигателя. Представим

qtj,p-t,p-\-\ r?p2 + 2,V+l

где Tl = VяТлТг, Тс,= /TJ; Si

2л/дТТ,

=2 -

2 л/Тм Т,

Частота свободных упругих колебаний Юу двухмассовой системы, найденная из решения характеристического уравнения (2.23), будет

У . (2.24)

Исследования механической части ЭП промышленных агрегатов показали, что значение коэффициента демпфирования 1 составляет в среднем менее 0,1 [19], что дает возможность считать соу « 1/Ti.

Структурная схема (рис. 2.4, б) справедлива и для жесткой системы. Действительно, в жесткой системе Тс = О, Т О и передаточная функция, учитывающая влияние обратной связи по ЭДС двигателя, будет

ТшЕ ( яР - и + 1

где Тэм2 = TMS /(я,).

в работе [49] показано, что если частота среза токового контура, настроенного на оптимум по модулю, лежит, по крайней мере, на декаду правее частоты 1/Тэм, т. е. Тэм>20 Тг, то влиянием обратной связи по ЭДС двигателя (в жесткой системе) можно пренебречь. Если считать, что частота среза токового контура в общем случае равна 1/(«о22), то это условие может быть несколько расширено:

>-. (2.26)