Они подразделяются на две подгруппы: статические и инерционные.

К числу инерционных вариаторов скорости относятся те, работа которых основана на использовании сил инерции движущихся деталей, специально для этого предназначенных. В обоих подгруппах вариатор может обладать или не обладать идеальной характеристикой.

Характеристика вариатора называется идеальной в том случае, когда в пределах заданного диапазона регулирования обеспечивается постоянство мощности и числа оборотов двигателя при различных значениях крутящего момента на выходном валу.

Принятая классификация является упрощенной и не охватывает все возможные схемы и конструкции механических вариаторов скорости. Однако разнообразие существующих конструкций, применяемых и предлагаемых к применению, ею исчерпываются.

В заключение следует отметить, что большинство конструкций вариаторов имеют серьезные недостатки, особенно это относится •к вариаторам для мощностей выше 15-20 тт. Поэтому изыскание простых конструкций механических вариаторов, которые были бы надежны в работе и позволяли передавать большие мощности, является проблемой сегодняшнего дня.

Глава первая

ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ ВАРИАТОРОВ СКОРОСТИ С НЕПОСРЕДСТВЕННЫМ КАСАНИЕМ РАБОЧИХ ТЕЛ

1. ВАРИАТОРЫ, У КОТОРЫХ ОБРАЗУЮЩАЯ КАТКОВ ЯВЛЯЕТСЯ ПРЯМОЙ ЛИНИЕЙ

Определение передаточного отношения вариатора скорости

Рассмотрим передачу вращения коническими катками (рис. 2, а) при условии, что буксование отсутствует и вершины О и образующих конусов не совпадают, причем вершина ведущего конуса Oj расположена на образующей ведомого конуса, т. е. расстояние между вершинами конусов положительное

a = 00i> 0.

Изменение передаточного отношения ti , = - вариатора осу-

ществляется перемещением ведущего катка / вдоль образующей 05 ведомого катка 2.

Вследствие несовпадения вершин конусов только в одной из. точек касания (точке К) окружные скорости катков 1 а 2 будут равны. Во всех остальных точках касания происходит неизбежное скольжение и износ катков. Кроме того, тела вращения, соприкасающиеся в начальный момент по линии, после приложения внешних сил деформируются и соприкасаются по некоторой площадке шириной t (рис. 3).

Давление р на площадке контакта, по теории Герца, изменяется по полуэллипсу, а элементарные силы трения, возникающие вследствие скольжения, прямо пропорциональны давлениям и не параллельны между собой. При вращении катков равнодействующая давлений смещается относительно плоскости XOZ и создает сопротивление перекатыванию.

Задача определения действительных радиусов качения катков с учетом распределения давлений по полуэллипсу [27] приводит к необходимости пользоваться номограммой, построенной для этой цели, и решение ее не дает общей аналитической зависимости.

Исследованиями [27] также установлено, что для часто встречающихся в практике соотношений размеров контактной площадки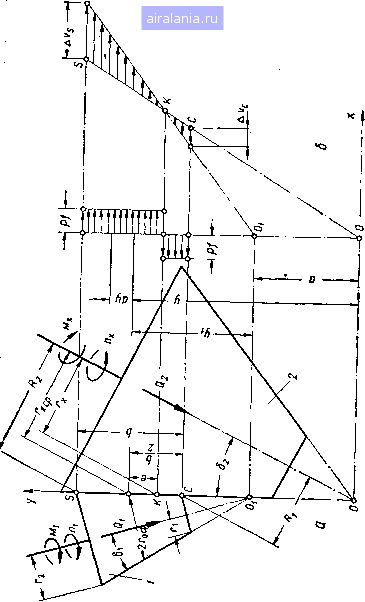

>> m

"8

3"

s

§ as

с та

s a.

y, не превышающих 0,25, можно без больших погрешностей для

инженерных расчетов решать задачу, считая, что все силы трения параллельны между собой и перпендикулярны к образующей катков.

В соответствии с изложенным в решении поставленной задачи приняты следующие допущения: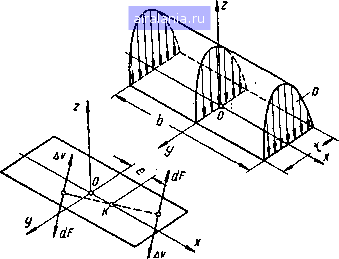

Рис. 3. Схема распределения давлений на площадке контакта.

сопротивление перекатыванию (от упругих сил - не учитывается) незначительно;

элементарные силы трения параллельны между собой и перпендикулярны к образующей по линии касания;

сила нажатия, расположенная нормально к образующей катков, распределяется по длине b контактной линии равномерно, скорости обоих катков равны в точке К.

Радиус г. (см. рис. 2, а) начальной окружности ведомого катка 2 определяют из условия его равновесия. На рис. 2, б показан график изменения скорости скольжения

До = - v,

а также график сил трения pf, отнесенных к линии касания катков.

Следует отметить, что направление момента сил полезных сопротивлений противоположно направлению вращения ведомого катка 2, а силы трения pf противоположны направлению относительного скольжения. Так например, для ведомого катка 2 силы трения на участке SK направлены в сторону вращения, а

на участке КС - в сторону, противоположную направлению вращения.

Для ведущего катка / - наоборот: силы трения на участке SK направлены в сторону, противоположную направлению вращения, а на участке КС - в сторону вращения.

При условии равномерного вращения уравнение моментов сил, приложенных к ведомому катку, имеет вид

Д. Гх

sins, sin

~M,-i- ] pfysm\dy- J pfysm\dy==0, (1.1)

sin 6, sin 5,

где P ~ ~b ~ rSnl--давление на единицу длины катка;

f - коэффициент трения поверхностей катков (табл. 1); S, - угол образующей ведомого конуса; /?2, и R[ - соответственно наибольший, начальный и наименьший радиусы окружностей катка в пределах контактной линии.

Таблица 1

Значения коэффициента / трения скольжения во фрикционных передачах

Наименование материала и условия смазкн

Сталь по стали со смазкой......

» » » или чугуну всухую . » . » текстолиту или фибре всухую » или чугун по коже всухую ....

» по ферродо всухую.......,

» или чугун по резине всухую . . » » » » дереву » ...

Сталь - бумага в питающих приспособлениях

Резина - бумага..............

Латунь с рифленой поверхностью - бумага

0,04-0,05 0,15-0,20 0,20-0,25 0,20-0,35 0,30-0,35 0,35-0,45 0,35-0,5 0,20 0,40 0,40

Подставляя значение р в уравнение (1.1), после интегрирования и преобразований получаем

= 2тда;1( + -2 (1-2)

Из рис. 2, а видно, что

= г, CP - 4 2.

где /-jc ср - средний радиус катка. 12

Заменяя л ъ формуле (1.2) их значениями, имеем

CP (у sin

fcsin*52

Решая уравнение (1.3) относительно г, получаем

(1.3)

X ср

Условие равновесия ведущего катка / при равномерном его вращении определяется из уравнения моментов

sin 6, sin 5,

- Ml- J piys\n\dy + J pfysinbdyQ. (1.5)

sin 6, sin 6j

После интегрирования, подстановки значений

Р-ьШь/ 2 = -ocp + ySin8j; /-1-Vp--sin8,

и ряда преобразований получаем

i = FlOT,hcp+(sin8,f-,J. (1.6)

где Ло, Tj, A-j, Гцср - соответственно начальный, наибольший, наименьший и средний радиусы ведущего катка; 5 - угол образующей конуса катка. Решая уравнение (1,6) относительно радиуса Гд, имеем

Радиус Го при известном определяется также из равенства, составленного в соответствии с рис. 2, а,

Гх „ Го ,

sin 82

откуда

Передаточное отношение вариатора

ffl £х

rxSlnS2

(1.8)

(1.9)

"х <»л г а (гя - а sin S2) sin 81

где определяется по формуле (1.4), а г„ - по формуле (1.8).

Анализируя формулу (1.4), можно видеть, что радиус начальной окружности ведомого катка равен среднему радиусу /,:cp при следующих условиях:

(1.10)

(1.11) (1.!?)

4 ~ Qr sino„ = 0; 6 = 0.