Для первой передачи (рис. 65, б) по формуле Виллиса получаем

"1 - "5 rjR,

«7 - Пь

При «7 = 0 имеем

п. =

«1

Для второй передачи запишем

"1 -"5

«2 - "5

(3.49)

откуда

n, = - n,

rji I

Подставляя значения щ из формулы (3.49), после преобразований получаем

(3.50)

По схеме на рис. 65, б видно, что

1 = РшС05(х, г* = piuSin (а + Р), /" = psin (cf-а). Подставляя эти значения в формулу (3.50), имеем

1 [ 7 COS g

I = 1 sin (я 4- p)

J ;?7 sin (y-a)

Ri sin (a-fp)

В частном случае, при tf = Р и = i?,, формула (3.51) приобретает вид

cos а

(3.51)

Г1 sin (а -f у) sin (у -а) Sin(cp-l-a)

Рассматриваемый вариатор строится с диапазоном регулирования от -}- 10 до - 6.

Глава четвертая

ВАРИАТОРЫ СКОРОСТИ С ПРОМЕЖУТОЧНЫМ ГИБКИМ ЗВЕНОМ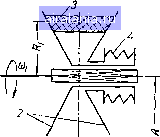

1. ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ ВАРИАТОРА С КЛИНЧАТЫМ РЕМНЕМ И РАЗДВИЖНЫМИ ШКИВАМИ

Вариаторы с клинчатыми ремнями и раздвижными шкивами получили широкое применение в промышленности, так как в большинстве случаев они просты по конструкции, бесшумно работают, не требуют большого первоначального натяжения ремня, надежны в работе, скорость ведомого вала легко и просто регулируется во время работы вариатора. Большое разнообразие существующих конструкций шкивов, различные сочетания сдвоенных вариаторов, а также сочетания клино-ременного вариатора с различными схемами зубчатых передач, позволяют легко выбрать одну наиболее рациональную из числа существующих схем в соответствии с заданной мощностью и с необходимым диапазоном регулирования скорости.

Принципиальная схема наиболее простого вариатора показана на рис. 66. Раздвижной шкив 2 состоит из двух дисков переменного диаметра, шкив / - постоянного диаметра. Регулирование угловой скорости ведомого вала осуществляется изменением расстояния А между осями шкивов (при постоянной длине ремня) путем перемещения одного из валов, обычно вала двигателя. С увеличением межосевого расстояния ремень 3, натягиваясь, разводит диски шкива 2 и огибает их по дуге окружности меньшего диаметра.

Рис. 66. Схема клииоре-менного вариатора с раздвижным шкивом.

При уменьшении межосёвого расстояния ремень под действием пружин 4 перемещается на больший диаметр. Сила трения между ремнем 3 и шкивами обеспечивается силами упругости пружин 4, расположенных на шкиве 2 по окружности, описанной из центра вала.

Шкив 2 устанавливается на вал со скользящей шпонкой, что дает ему возможность перемещаться вдоль осиала и самоустанавливаться в положение, соответствующее средней плоскости движения ремня.

Определение усилий, действующих на пружины

В принятой теории ременных передач на дуге в пределах угла обхвата а различают: 1) дугу скольжения, расположенную со стороны сбегающей ветви, в пределах которой происходит упругое проскальзывание ремня по шкиву; 2) дугу покоя, расположенную со стороны набегающей ветви, в пределах которой ремень, сохраняя первоначальное натяжение, не деформируется и не проскальзывает.

Нормальное давление (рис. 67, а) и его составляющая

2tgY

, которая действует на диск параллельно оси вала, оп-

ределяются в соответствии с условиями работы ремня на дуге покоя и на дуге скольжения. Суммарное усилие, действующее на диск, равно

Т = Т,. + Тп,, (4.1)

где Гек - усилие, возникающее в пределах дуги скольжения; Гпк -усилие, возникающее в пределах дуги покоя. В пределах угла покоя радиальная составляющая Quk определяется из условия постоянства натяжения S ремня. В соответствии с рис. 67, б имеем

dQ„k = 2S sin Y

Принимая sin у = у и интегрируя в пределах угла (угла покоя), получаем

QnK " -ПК

Составляющая Т„к, действующая параллельно оси вала, с учетом сил трения, направленных вдоль образующей, определяется из параллелограмма сил (рис. 67, в) и равна

"" (4.2)

где 2y - угол желоба шкива; р - угол трения.

2tg(Y+p)

Для ведущего шкива в формулу для Тпк следует подставить значение натяжения 5, - ведущей, а для ведомого шкива -S - натяжение ведомой ветви ремня. Поэтому усилие, действующее вдоль оси вала ведомого шкива, всегда меньше усилия, действующего вдоль оси вала ведущего шкива, так как > S..

Определение угла покоя апк связано с рядом затруднений. Поэтому усилие Т рекомендуют [31] определять по усилию Гек, принимая коэффициент надежности для ведущего шкива р= 1,5--2, для ведомого р = 1,2 -ь 1,4 и апк = 0.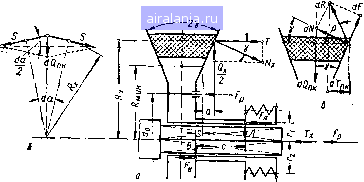

Рис. 67. Схема сил, действующих на двухдисковый шкив кли-ноременного вариатора.

Зависимость между натяжениями Sj и определяется известной формулой Эйлера

(4.3)

где е -основание натуральных логарифмов; / = - приведенный коэффициент трения;

/ - коэффициент трения скольжения ремня по шкиву; а - угол обхвата. Значения величин el" даны в табл. 9.

Сила трения между шкивом и ремнем при постоянном крутящем моменте на валу должна быть равна

(4.4)

где Мкр1-крутящий момент на валу рассматриваемого шкива; х -радиус, равный расстоянию от нейтральной линии ремня до оси вращения шкива; -окружное усилие,

Значения e"

Таблица 9

Угол обхвата

Отношение дуги обхвата к окружности

Коэффициент трения f (приведенный)

0,25

0,35

0,45

36 72

108 144 153 162 171 180 189 198 216 252 288 324 380

0,425

0,45

0,475

0,525

0,55

1,13

1,29

1,45

1,65

1,76

1,82

1,87

1,93

2,00

2,13

2,41

2,75

3,51

1,17

1,37

1,87

1,95

2,03

2,11

2,19

2,28

2,37

2,57

3,51

4,11

4,81

1,21

1,46

1,76

2,18

2,23

2,34

2,45

2,57

2,69

2,82

3,74

4,52

5,45

6,59

1,25 1,56 1,93 2,41 2,55 2,69 2,84 3,00 3,17 3,35 3,74 4,66 5,81 7,24 9,02

1,29 1,65 2,13 2,73 2,91 3,1 3,3 3,51 3,74 3,98 4,52 5,81 7,47 9,6 12,35

1,33 1,76 2,34 3,1 3,33 3,57 3,83 4,11 4,41 4,74 5,45 7,24 9,6 12,74 16,9

1,37 1,87 2,57 3,51 3,8 4,11 4,45 4,81 5,2 5,63 6,59 9,02 12.35 16,9 23,14

В соответствии с рис. 67, а равнодействующая радиальных давлений ремня на щкив равна

Подставляя значение из уравнения (4.4), получаем

(4.5)

Рассматривая равновесие правого диска шкива в момент перевода на меньший диаметр (рис. 67, а), устанавливаем, что нормальное давление ремня уравновешивается силами упругости

пружин, силами трения Fa и Fb, которые возникают между направляющими поверхностями ступиц дисков от силы N, и силами трения F„ на направляющих пальцах от половины крутящего момента Л1кр1. Силы трения F, Fa и Fb направлены в противоположную сторону движения диска. Считая, что равнодействующая Гд. сил упругости пружин и равнодействующая Fp приложены по оси вала, составляем уравнения моментов всех сил и определяем опорные реакции А и В. Затем, проектируя все силы на горизонтальную ось и подставляя значения опорных реакций, после ряда преобразований, получаем;

1. Для случая, когда правый диск перемещается слева направо

ТА+Гх (то - -о)] = [ 1 + Г1 (то - k,) + R,, tg f (m.+k,) -

- 5 tg 7 (mo + k,) + moc tg т] - Jt {Шо + *o) - (4-6) - fp[+ri (mo --to)],

мин - минимальный радиус шкива; i, с и 5 -размеры ступицы правого диска (рис. 67, а);

где г

" *o = q-коэффициенты;

1J. - коэффициент трения скольжения между трущимися

Рр =

поверхностями ступиц дисков; --J- - сила трения;

-диаметр окружности, по которой расположены направляющие пальцы; [Хд - коэффициент трения скольжения между направляющим пальцем и подвижным диском. Подставляя значение из формулы (4.5) и обозначая постоянные величины через

Ео=1+г (то - /о) + мин tg2Y + о) -5 tgf (mo + k) + и +moCtgY

получаем

D,= l+r, (mo-/%o),

2RxDor tg 7

(4.7)

2. Для случая, когда правый диск перемещается справа налево, знак перед и изменяется на обратный.

Анализируя формулы (4.6), (4.7) и величины Шо и йц, которые в них входят, можно установить, что при с = 2[АЛ1 подвижный диск заклинивается. Для приближенных расчетов можно принять в формуле (4.7) Е(,= I и Dq = 1.

Из формулы (4.7) также видно, что в случае значительной перегрузки вариатора, превышающей принятое значение коэффициента ремень может автоматически развести диски шкива и «уйти* на меньший диаметр при неизменном расстоянии между центрами шкивов.

В соответствии с изложенным при проектировании привода вариатор следует устанавливать в числе первых передач от вала двигателя в кинематической цепи передаточного механизма.

Определение размеров пружин

Диаметр d проволоки круглого сечения винтовой пружины определяется по условию прочности;

1=1,6]/

TiCk

гн:- (4.8)

где Z -число пружин;

Ti -максимальное усилие, действующее на пружины, определяемое по формуле (4.6) при R = /?„„„;