Условие (1.10) в общем случае практически никогда не выполняется, так как при нажатии катков с большой силой, равной

понижается коэффициент полезного действия вариатора, увеличиваются износ, трущихся поверхностей и габарить* всего механизма.

Условие (1.11) соответствует цилиндрической форме катков,, а условие (1.12) - касанию катков по бесконечно малой длине образующей (например, в интеграторах).

Формулу (1.4) удобнее анализировать, переписав в виде

X ср

/, b sin \ /Мх sin 52 fesin8a\ , ,„

Обозначая

Мх sin 52

и решая это равенство относительно Q, получаем

Мх sin 52 Q

xcpl

(1.14)

Это известная формула, которой пользуются при расчетах в случае совпадения вершин образующих конусов, где р - так называемый коэффициент надежности.

Подставляя у в формулу (1.13), имеем

1 sin bo

l\ ftsinBjX

(l.!5)

В соответствии с (1.7) для радиуса начальной окружности ведущего катка*" / получаем

По формуле. (1.15) радиус начальной окружности ведомого катка в случае смещения вершин конусов равен среднему радиусу при условии

Ъ sin \

(1.17)

X Ср

В заключение следует отметить, что, как правило, размеры катков существующих и проектируемых вариаторов скорости удовлетворяют неравенству

1 fcsinbj

«ср

поэтому радиусы начальных окружностей катков при расположении вершины ведущего конуса на образующей ведомого всегда меньше средних радиусов.

Небезынтересным является рассмотрение случая холостого хода. По формуле (1.4) при Л!,, = О

(1.18)

так как

Ь sinBa"

В рассматриваемой схеме вершина 0 конуса ведущего катка расположена выше оси X и отрезок OOj считается положительным. Если Oi ниже оси X (рис. 4), то картина относительного сколь-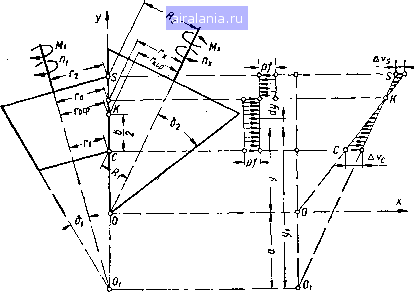

Рис. 4. Схема скольжения по линии контакта при расположении вершины ведомого конуса на образующей ведущего.

жеиия и положение радиусов начальных окружностей и Го изменяется.

Как и прежде, составляя уравнение моментов сил, приложенных к ведомому катку, получаем

R, г„

sin 6j

sin 6,

sin 5,

sin 6,

- - J Py sin \dy + J pty sin S,dy = 0. (1.19)

После интегрирования и преобразований, произведенных подобно тем, которые были сделаны в первом примере, получаем:

Ь sin* 62

/ , b sin 5; / 1 b sin f>i\

Для ведущего катка имеем:

= [rg-(isin5,)-.gep

/, , »sinSi / 1 , iS>sin6

(1.20) (1.21)

(1.22) (1.23)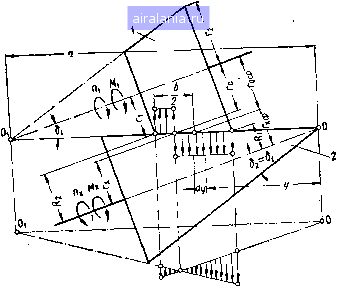

Рис. 5. Схема скольжения по линии контакта конусов, когда их вершины, ваправлены в разные стороны.

•Радиус начальной окружности ведущего катка определяется также в зависимости от в соответствии с рис. 4:

(1.24)

/ 1 • ч sin S, ro = ( + asin8,)-j-y.

sin 62

Анализ формул (1.21) и (1.23) показывает, что радиусы начальных окружностей ведомого и ведущего катков при расположении вершины ведомого конуса на образующей ведущего всегда больше средних радиусов, даже при коэффициенте надежности

Р = 00.

Из изложенного вытекает, что при передаче вращения коническими фрикционными катками, проектируемыми с совпадением вершин конусов, в случае даже незначительного смещения ( +Да) происходит изменение радиусов начальных окружностей катков. -Передача в этих условиях работает с неустойчивым передаточным отношением.

Выше рассматривались схемы вариаторов с катками, вершины образующих конусов которых направлены в одну сторону. Не исключена возможность расположения вершин конусов в разные стороны (рис. 5). Регулирование скорости при данной схеме может осуществляться перемещением катков вдоль оси вала при соответствующем изменении расстояния между валами.

Углы §1 и §2 образующих конусов в рассматриваемом случае могут быть равными при параллельном расположении осей валов и различными при непараллельных валах. Результаты выводов не зависят от того, какая из схем рассматривается, так как условие равновесия каждого катка записывается отдельно.

Как и прежде, определяя радиусы начальных окружностей катков по уравнению моментов сил, получаем для ведомого катка формулу (1.21) и для ведущего - формулу (1.16), из которых видно, что при расположении вершин конусов в разные стороны радиус Начальной окружности ведомого катка всегда больше среднего, а ведущего - меньше среднего радиуса.

При известном радиусе начальной окружности ведомого катка радиус Гц ведущего катка в соответствии с рис, 5 определяется также по формуле

г г, =

sin 62/

sinSi.

Определение максима.ьной скорости скольжения в зоне контакта рабочих тел

Как указывалось выше, качение катков без скольжения происходит по начальным окружностям радиусов Го и г; все другие точки касания в зоне контактной поверхности имеют разные скорости, вследствие чего происходит неизбежное скольжение и износ катков.

Величина скорости скольжения До = Di - изменяется по закону прямой (см. рис. 2) и имеет максимальные значения в точках, граничащих с максимальным и минимальным радиусами одного из катков, ограниченного по ширине размером Ь.

Для ведущего катка 1 скорости точек С и 5 соответственно равны

и для ведомого катка 2 где u)j и u)j5 - угловые скорости катков 1 я 2.

2 171 5=.

Максимальная скорость скольжения в точке С равна

Дос=УС2 -(Ь25)

и в точке S

vs-=vs, - vs. (1.26)

Подставляя значения скоростей, заменяя

О)] Г„

1-2 X

И пользуясь формулами (1.8) и (1.24), после преобразований получаем:

п (гх±а sin 82) sin

Al - --Г,

Дох = (Oj В формуле (1.27)

rxSlnOj

(Гж ± а sin bj) sin b,

Гд; sin bj r, = - 6 sin \.

(1.27) (1.28)

Из формул (1.27) и (1.28) следует, что при всех прочих равных условиях скорости скольжения увеличиваются с увеличением смещения а вершин конусов.

Определение к. п. д. вариатора скорости

Полный коэффициент полезного действия вариатора скорости, как и к. п. д. любого механизма, определяется отношением работы сил сопротивления, приложенных к ведомому звену, к работе движущих сил, приложенных к ведущему звену. Таким путем учитываются потери на преодоление всех вредных сопротивлений, возникающих в кинематических парах системы рассматриваемого вариатора: трение в подшипниках, трение качения в зоне контакта фрикционных катков и др.

Наиболее приемлемым в практике методом вычисления к. п. д. является приближенный метод: сначала определяют реакции в кинематических парах без учета сил трения, а затем по найденным реакциям - работу сил трения и к. п. д. механизма.

Считая решение этой задачи общеизвестным, рассмотрим только определение потерь на трение скольжения по линии касания катков.

Воспользуемся известным соотношением между крутящими моментами ведущего и ведомого звеньев механизма

откуда 18

где Tj - коэффициент полезного действия механизма; ii 2- ~ - передаточное отношение.

Крутящие моменты и при положительном смещении вершин конусов соответственно определяются по формулам (1.3) и (1.6), при отрицательном смещении -по формулам (1.20) и (1.22).

Подставляя в формулу (1.29) значения М, Mi,./i 2h Qj =

~2sfn" "-" преобразований получаем

Го sin bj

(ysinbj)

rsinSa

(Asin5,)

(1.30)

Го = (г, Та sin 8,)-

sin 61 sinb,

Верхние знаки относятся к случаю положительного смещения вершин конусов, а нижние - к случаю отрицательного смещения.

Для схемы вариатора, у которого вершины конусов направлены в разные стороны, числитель формулы (1.30) имеет нижние знаки, а знаменатель - верхние.

Частные случаи схем вариаторов

Рассмотрим некоторые частные случаи схем вариаторов, у которых вершины конусов направлены в одну и в разные стороны.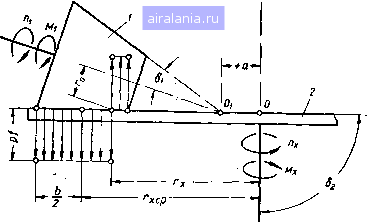

Рис. 6. Схема направления сил трения при bj = 90°.

Изменяя угол образующей ведомого конуса в сторону его увеличения до = 90°, получим схему механизма, которая представлена на рис. 6.