Формулы (1.15) и (1.21) для рассматриваемого случая будут иметь вид

При положительном смещении вершины 0 ведущего конуса; которое .соответствует расположению катков на рис. 6, следует в формуле (1.31) принять верхние знаки, а при расположении вершины Oj справа от О - нижние знаки.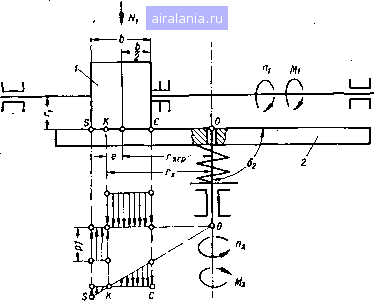

Рис. 7. Схема скольжения по линии контакта лобового вариатора

скорости.

В промышленности для передачи небольших мощностей применяется вариатор, схематически изображенный на рис. 7. Рассматриваемая схема представляет собой частный случай, соответствующий условиям: §2 = 90°, 8j = О, вершина ведущего конуса удалена на а= ± оз.

Крутящий момент на ведомом валу в данном случае определяется по формуле (1.20), а радиус окружности катка 2 - по формуле (1.21).

Крутящий момент Mj на валу ведущего катка 1 определяется по уравнению моментов сил

где 20

I xzp

Решая уравнение моментов сил относительно М, имеем

Mi = 24-.-r«p). (1.32)

Подставляя в формулу (1.29) по формуле (1.20), .М по

формуле (1.32), ii 2 = и Al = = Q2. получаем

Как* видно из формулы (1.33), -ц не зависит от г.

(1.33)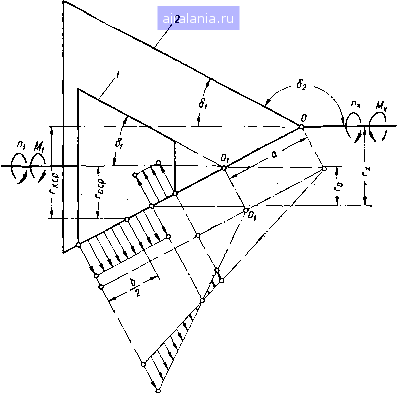

Рис. 8. Схема скольжения по линии контакта при Ь. > 90.

Увеличивая угол 82 образующей ведомого конуса до величины, большей 90°, получаем вариатор скорости с одним внутренним и другим внешним конусами (рис. 8 и 9). В большинстве случаев такие вариаторы строятся с параллельным расположением осей валов, поэтому

sin 81 = sin 82, 8 + 82 = 180°. . .

Формула (1.15), определяющая радиус ведомого катка, остается в силе, так как смещение вершин конусов положительное.

Средний радиус Госр ведущего катка у вариатора на рис. 8 постоянный, ведомого - переменный; на рис. 9 - наоборот. Размеры радиусов связаны зависимостью

Го = - а sin 8i.

Размещая два механизма, у которых вершины конусов направлены в разные стороны симметрично относительно оси А -А (рис. 10), получим схему вариатора скорости с взаимным уравновешиванием осевых усилий Q. Пружина 3 прижимает катки 1 и 2 с силой, достаточной для передачи вращения, и компенсирует износ их. Регулирование скорости осуществляется изменением расстояния А между осями валов. Заменяя подвижное соединение катков вдоль осей валов неподвижным, получим обычную фрикционную передачу с цилиндрическими клинчатыми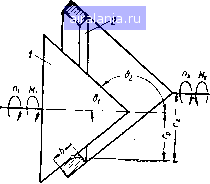

Рис. 9. Схема вариатора с постоянным средним радиусом ведомого и переменным радиусом ведущего катков.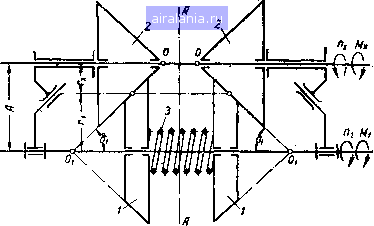

Рис. 10. Схема! сдвоенного вариатора скорости, у которого вершины конусов направлены в разные стороны.

катками. Радиусы начальных окружностей катков определяются по формулам (1.21) и (1.16).

Определение коэффициента скольжения вариатора

Как было установлено выше, действительное передаточное отношение = - вследствие скольжения по линии контакта отлц-

чается от передаточного отношения = --, определяемого по

средним радиусам и зависит от коэффициента надежности реактивного момента на ведомом валу и геометрических параметров вариатора. Очевидно, скольжение и все связанное с ним (износ, к. п. д., нагрев и др.) будет тем больше, чем больше отличается /i 2 от il-2.

Для сравнительной качественной оценки вариаторов скорости принято пользоваться так называемым коэффициентом скольжения, который определяется зависимостью

s= 1 -

(1.34)

Подставляя значения радиусов г, и Го в соответствии с (1.15), (1.21), (1.16) и (1.23) в (1.34), после преобразований получаем

s= 1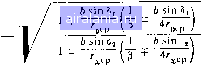

(1.35)

Знаки минус относятся к случаю, когда вершина ведущего конуса расположена на образующей ведомого.

При расположении вершин конусов в разные стороны в верхней строчке следует поставить знаки минус, а в нижней - знаки плюс. Следует заметить, что в последнем случае коэффициент скольжения получается более высоким, а к. п. д. более низким, чем при расположении вершин конусов по одну сторону контактной площадки, при которых коэффициент скольжения е составляет примерно 2 - 5%.

Для лобового вариатора скорости (см. рис. 7) коэффициент скольжения

е = 1

ccpl

Г1Гх

хер Гх

Подставляя значение г в соответствии с формулой (1.31) при 82 = 90°, получаем

1±1

L V

4г

(1.36)

Знак плюс относится к случаю, когда каток / является ведущим, и знак минус -когда ведомым. Как видно из формулы (1.36), с уменьшением гср коэффициент скольжения возрастает.

35 30 25 20 15

Рис. 11. График изменения коэффициента скольжения лобового вариатора.

На рис. И дан график изменения s в зависимости от гжср при fc = 20 мм и р = 1,2.

2. ВАРИАТОРЫ, У КОТОРЫХ ОБРАЗУЮЩАЯ КАТКОВ ЯВЛЯЕТСЯ ДУГОЙ ОКРУЖНОСТИ

Определение линейных давлений в зоне контакта рабочих тел

В современном машиностроении широкое применение получили вариаторы скорости с катками, рабочие поверхности которых образованы вращением дуги окружности относительно осей валов. На рис. 12, а показана схема такого вариатора. Передача движения от одного катка к другому осуществляется силами трения, возникающими по контактной линии ВН вследствие прижатия катков друг к другу с достаточной силой. Последнее можно осуществить перемещением катка /, перемещением катка 2 или одновременным перемещением обоих катков вдоль их осей вращения.

Каток /, так же как и каток 2, может быть ведущим или ведомым. Передаточное отношение вариатора изменяется поворотом вала катка 2 относительно оси, перпендикулярной к плоскости чертежа и проходящей через точку 0.

Скорости точек катков по дуге касания различны, поэтому неизбежны скольжения катков, износ их и потери мощности на трение. С уменьшением ширины Ь катка 2 скольжение уменьшается, но увеличивается давление р по контактной линии, которое не должно превышать допускаемых значений, зависящих от материала катков.

Как и в предыдущей задаче, допускаем, что давление распределяется не по площадке, а по линии. Однако в зоне контактной

линии рассматриваемого вариатора линейное движение распределяется неравномерно, особенно при большой ширине катка 2. Кроме того» максимальное давление возникает в одной из крайних точек и или В линии контакта и зависит от того, перемещением какого катка {1 или 2) осуществляется необходимое нажатие, обеспечивающее работу вариатора без буксования. Следует также заметить, что давление между катками должно быть больше необходимого (расчетного) на 15-20%.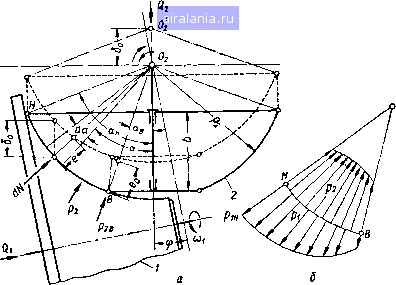

Рис. 12. Схема распределения линейных давлений при перемещении катка 2 и неподвижном катке /.

При большом же значении давления будут происходить излишние затраты энергии на преодоление трения, возникающего вследствие неизбежного геометрического скольжения, и ряд других нежелательных явлений.

В современных конструкциях рассматриваемого вариатора давление между катками осуществляется перемещением катка / силой Qi, при этом наибольшее давление pui всегда будет возникать в точке Н, более удаленной от оси вращения катка 5, и наименьшее - в точке В (рис. 12, б). Неравномерность распределения давления зависит от положения оси вращения катка 2 и наиболее неблагоприятной бывает при наибольших значениях передаточного отношения.

Боле рациональным для рассматриваемого вариатора (8) следует считать прижатие катков посредством перемещения катка 2 с силой (?2- этом случае неравномерность распределения линейного давления Ра (Рис. *12, б) не зависит от положения катка 2