Передача масла к тому или иному поршню определяется положением золотника (рис. 147), который связан с пультом программного управления.

Рассматриваемая система регулирования скорости может быть применена для условий, соответствующих работе одношпиндель-ного автомата.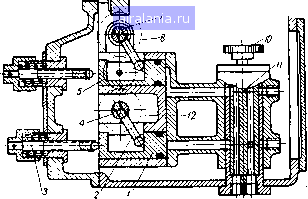

Рис. 147. Схема гидравлического механизма управления вариатором.

Следует также отметить, что данный вариатор не пригоден для работы с реверсивным движением.

Изменение технологии производства влечет за собой только перестройку положений упоров 3.

Определение сил, действующих на ролик при параллельном расположении его оси относительно линии центров дисков

На рис. 148, а показана схема лобового вариатора. Диск/ - ведущий, ролик (расположенный под диском) -ведомый. Из графика скоростей скольжения видно, что в любой точке касания результирующая скорости скольжения может быть разложена на две составляющие, одна из которых направлена по касательной к окружности ролика, а вторая - параллельно его оси.

Скорость по касательной в одной из точек по линии контакта равна нулю, максимальные же значения соответствуют крайним точкам. Ограничивающим ширину ролика. Скорости скольжения, направленные параллельно оси ролика, в любой точке равны

Оо = = const,

где Е - величина смещения оси ролика; ш, - угловая скорость ведущего диска /.

Максимальная скорость скольжения по касательной в точке а определяется разностью скоростей

где Uap = о)р Го - скорость ролика;

* I составляющая скорости диска;

о)р = - угловая скорость ролика;

Го - радиус ролика; Ъ - ширина ролика;

е -величина смещения (от средины ролика) точки k касания ролика с диском, в которой скорость скольжения по касательной равна нулю;

/ - радиус, определяющий положение точки k.

Подставляя значения у„р и t»„i в формулу (6.1), получаем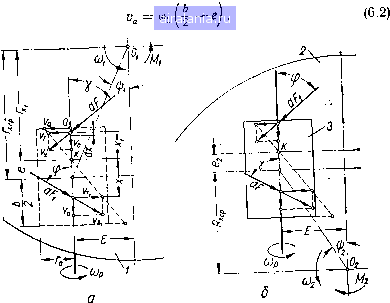

Рис. 148. Схема сил, действующих иа ролик лобового вариатора с перекрещивающимися осями валов при холостом ходе.

Скорость скольжения по каЬательной в произвольной точке касания определяется из соотношения

- fa

Подставляя значение t>„ по формуле (6.2), имеем

(6.3)

Положение результирующей скорости скольжения и силы трения dF в произвольной точке касания определяется по схеме (рис. 148, а).

Соответственно

(6.4)

dF cos ср.

(6.6)

Точно такие же соотнощения получим, рассматривая лобовую фрикционную передачу (рис. 148, б), когда ролик 5 является ведущим, а диск 2 - ведомым.

Суммарная составляющая сил трения, приложенных к ролику, направлена вдоль его оси и при работе вариатора вхолостую равна

So = S + S, (6.5)

5з= j dFcosj и 5 =

Обозначая силу прижатия диска / к ролику 3 через .Q, определим элементарную силу трения

dF,=dF = fpdx = fdx. Подставляя значения dF и dF в формулы (6.6) и заменяя

после интегрирования и преобразований получаем

, (6 -2в)+ \/iE + {b - 2ef , 2£ +

, . (b + 2е) + V4E + (b + 2ef -jr III

2-Е-• (6-7)

Величину 5(, с достаточным приближением можно определить при е = О, тогда

o-Q-fe In-2-.

(6.8)

Для ролика, зажатого между двумя дисками 1 я 2, как это имеет место в рассматриваемой схеме, получаем

S„ = 4Q/ln±iil±=4Q/C.

(6.9)

!Д1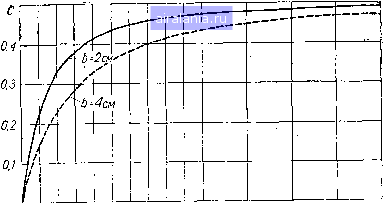

О 0.2 0.4 0.6 0.8 1 12 14 16 18 2 2.5 3 3.5 Е см Рис. 149. График зависимости С = f (Е) при 6=2 см и при 6 = 4 см.

Значения С = f(Е) при & =:2ш и & = 4слг даны на графике (рис. 149),

Формула (6.9) определяет усилие 5о, приложенное к ролику при холостом ходе и направленное вдоль его оси. При работе над нагрузкой крутящий мо- -ч

мент М, приложенный к f„

диску /, и реактивный мо- Л,

мент, приложенный к диску 2 (рис. 150), также создают усилия, приложенные к ролику, а их составляющие, направленные вдоль оси, определяются из равенств (рис. 150):

Sm, = cos sin ==

M, tgL (6.10)

•Sm, = #cos2sin2 =

M2 tg Ф;

(6.11)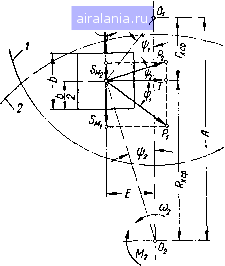

(J „ /К 19\ Ри- 50. Схема сил, действующих на

ом - "JjM, OjM,. (D-l-) ролик вариатора от внешних моментов.

Без учета к. п. д. вариатора момент на ведомом диске 2 равен

д:ср

(6.13) 191

Подставляя значения Sm, и Sm. в формулу (6.12) и заменяя по формуле (6.13), после преобразований имеем

Sm =

Из рис. 150 находим

tg ti = и tg 2 = ;

Е . . Е

хер

Подставляя эти значения в формулу (6.14) и обозначая /?хср : /*cp=t и соответственно Гхср = j-qjj, получаем

8м = М,Е{1 +

-0,!8~ -0,165

-0.12-

0.09--0.075

I Уб /51/4 mWi

Е=2см

-Е-1см

Л2 +£2(1 ;)2

"Л+£2(1 f.

, (6.15)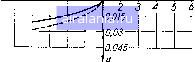

или Sm = Mi/.

Значение fy = /(t) для £•= 1 сл« и = 2 ш при А = 15 см даны на рис. 151.

Суммарное усилие, приложенное к ролику и направленное вдоль его оси, при передаче крутящего момента j равно

S = Sq Sm =

6 2£

-f Mi£(i + 1)

Рис. 151. Номограмма и = f (i) при £ = 1 сж и при £ = 2 сж.

АЧ + £2(1+ if

Л2 + £2 (J f. /)2

. (6.16)

Кроме осевого усилия, на ролик действует пара сил от составляющих, направленных перпендикулярно оси ролика. По рис. 148, а при е = О имеем

dMp, =2dFxi sin т = 2Q/Xj sin 7.

Заменяя

sinT- , = -7,

(6.17)

Получим

dMp, = 2Jf

xfdx

Ve +

(6.18)

Интегрируя полученное дифференциальное уравнение, после преобразований, имеем

f и -. / ттт Р2 £ \

Для рассматриваемого вариатора, когда ролик зажат между двумя дисками, получаем

f(b-/~ ГЛТ2 F2, £ \

j/..+(4)4fin

. (6.19)

3. ВАРИАТОР С ПЕРЕМЕННОЙ УГЛОВОЙ СКОРОСТЬЮ НА ВЫХОДНОМ ВАЛУ (ВАРИАТОР РЕТТИХА)

Ведущий вал 2 и ведомый 8 рассматриваемого вариатора (рис. 152) вращаются в одном направлении и за период одного оборота ведущего вала с постоянной угловой скоростью ведомый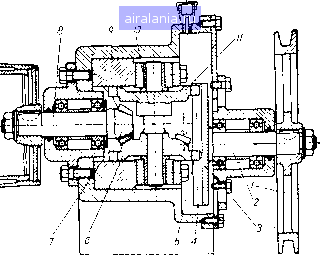

Рис. 152. Вариатор Реттиха.

также совершает один оборот, но с переменной угловой скоростью, изменяющейся по закону синуса.

Работа механизма осуществляется следующим образом. От шкива / клиноременной передачи движение передается ведущему валу 2, на котором жестко закреплена зубчатая рейка 3 в виде диска с зубьями 4, расположенными по всей плоскости диска.