Зубья 4 рейки находятся в зацеплении с зубьями 5 цилиндрических зубчатых колес и 6, причем колесо 6 выполнено заодно целое с коническим зубчатым колесом.

Ось 10 колес 11 и 6 установлена диаметрально в обойме 9 и вращается в подшипниках, а обойма 9 свободно вращается в корпусе вариатора. Зубья конического колеса находятся в зацеплении с зубьями конической шестерни 7, соединенной с выходным валом 8.

В том случае, когда эксцентриситет е равен нулю, ведущий вал 2 и ведомый 8 расположены соосно и вращаются как одно целое с постоянной угловой скоростью.

При смещенном расположении осей валов зубчатые колеса 6 и , кроме вращательного движения с обоймой 9, совершают еще колебательное движение относительно оси 10, которое сопровождается скольжением зубьев 5 относительно зубьев рейки 4.

Полный цикл вращения ведомого вала 8 с переменной скоростью по синусоидальному закону соответствует одному обороту ведущего вала. Наибольшие значения угловой скорости ведомого вала смещены по фазе на угол 180°.

Степень неравномерности вращения ведомого вала регулируется изменением эксцентриситета е.

Рассматриваемый вариатор может быть использован в установках для испытания абразивных камней на разрыв, а также в приспособлениях для снятия заусенцев и затупления острых кромок в окнах маслосъемных колец.

Глава седьмая

ВАРИАТОРЫ С АВТОМАТИЧЕСКИМ РЕГУЛИРОВАНИЕМ СКОРОСТИ В ЗАВИСИМОСТИ ОТ КРУТЯЩЕГО МОМЕНТА НА ВЕДОМОМ ВАЛУ

1. ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИКИ ЛОБОВОГО ВАРИАТОРА

Рассмотрим характеристику лобового вариатора по схеме, показанной на рис. 153 при условии, что ведущий диск / не меняет своего положения относительно оси промежуточного диска 2 (у = const), а ведомый диск 3, ступица которого соединена с выходным валом винтовой парой, перемещается вдоль оси в зависимости от крутящего момента М., сжимая при этом пружину. Мощность, передаваемая вариатором, равна

~ 71 620*

(7.1)

В соответствии с рис. 153 имеем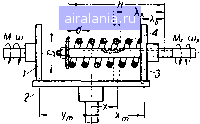

п пх

Рис. 153. Схема лобового вариатора с автоматическим регулированием скорости.

где п и - соответственно числа оборотов ведущего и ведомого валов вариатора в минуту.

Подставляя значение п, в (7.1), получаем

Осевое усилие винта, сжимающее пружину, определяется по формуле

r,ptg(=p-bp)-

Прогиб спиральной пружины с витками круглого сечения равен

reptg(=p + p) Gd*

(7.3)

где Гер -средний радиус резьбы вала;

tp-угол подъема винтовой линии резьбы; р - угол трения винтовой пары;

- прогиб пружины; Z - число витков пружины; D -средний диаметр пружины; d - диаметр проволоки пружины; G -модуль упругости второго рода. Формулу (7.3) перепишем в виде

X. = м,л,

где А - величина постоянная для данного вариатора.

Зависимость величины х от М. определяется из следующих условий (рис. 153):

= - (X;, - Хо) =х„ - М,А + МаА,

(7.4)

где x„j - расстояние, определяющее положение ведомого диска при номинальном крутящем моменте Mq на ведомом валу; Xq - прогиб пружины, соответствующий моменту М.

Подставляя значение д; в формулу (7.2), определяющую мощность, передаваемую вариатором, получаем

Ут71 620

- М.АМА).

(7.5)

Рис. 154. График изменения п, х иг в зависимости от Мх при ут = const, Mo= Л1 и Л = 0,00313.

Кривые изменения величин д; и / в зависимости от для данного вариатора при „ =10 см = const, Мр = М (момент на ведущем валу) и Л = =0,00313 приведены на рис. 154.

Из уравнения (7.5) и приведенного графика видно, что мощность, передаваемая вариатором по принятой схеме, не постоянна и изменяется по закону параболы. Очевидно, для того, чтобы мощность, передаваемую вариатором, получить постоянной, следует перемещать ведущий диск / {Ут Ф const), сохраняя при этом закон перемещения ведомого диска 3 (см. рис. 153) таким, как это было установлено в выше-рассмотренном примере.

Определим, как должна изменяться величина у„ при условии постоянства мощности без учета потерь.

По условиям статики поставленному требованию удовлетворяет равенство

м

Подставляя значение х из уравнения (7.4), получаем У={Хт-МхА + М,А).

(7.6)

(7.7)

При рассмотрении полученного уравнения видно, что величина у должна изменяться по закону параболы и в этом случае вариатор будет иметь идеальную характеристику.

Весьма существенным в рассматриваемой задаче является определение А, при котором у не выйдет за пределы конструктивно заданных размеров промежуточного диска 2.

Взяв производную -~ и приравняв ее нулю, определим значение М, при котором у будет максимальным.

-- = £ -I- Л - 2М = О, dMx М М -М

откуда

в 12 16 20 Mi км

Рис. 155. график зависимости Л, X я i в зависимости от Мх при изменении значения у по закону, соответствующему постоянству мощности.

Подставляя полученное значение Мх в уравнение (7.7), после преобразований имеем

У = (Хт + МоАГ. (7.8)

Здесь Мо определяется по формуле (7.6) при минимальном значении у = и максимальном значении х = Хт = Ут т. е.

Подставляя значение в формулу (7.8) и решая ее относительно А, получаем

(7.9)

A = -A(2-io) + 2Vl-io].

Кривые изменения величин х, у, N и i в зависимости от Мх приведены на рис. 155, из которого видно, что с увеличением Мх от Мо до Mm ведущий диск I (рис. 153) следует перемещать из положения, соответствующего минимальному значению у, в поло-1; жение, определяемое его максимальным значением Ут, а затем

возвращать в исходное положение.

Регулирование величины вручную затруднительно, особенно в тех случаях, когда необходимо установить ведущий диск с достаточной степенью точности. Это возможно, если заданный крутящий момент на ведомом диске не изменяется продолжительное время.

Указанный недостаток не имеет места, если изменить принципиальную схему вариатора так, чтобы ведомый диск получил перемещение не только за счет деформации пружины, но также и за счет перемещения опоры пружины в осевом направлении.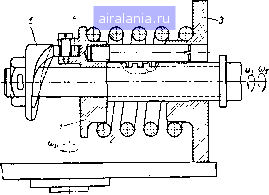

Рис. 156. Схема лобового вариатора с перемещающейся опорой пружины.

Конструктивная схема узла вариатора с перемещением опоры пружины показана на рис. 156. Диск 3, перемещаясь вдоль оси по нарезанной части вала, сжимает пружину 2 и поворачивает её опору /. Ролик 4, установленный на опоре пружины, перекатывается по торцу профилированной шайбы 5, а ведомый диск 3 при этом перемещается не только за счет деформации пружины, но и за счет перемещения ее опоры.

Сохраняя прежние обозначения и полагая, как в первом примере, что у = у = const, Мо = М и х„= Ут, напишем условие постоянства мощности, передаваемой вариатором, без учета к. п. д.

Мп = Мп = const.

В соответствии с поставленным условием размер х, определяющий положение ведомого диска 3 при заданном моменте М, определяется так:

Мут щ

Размер X, определяющий положение диска 5 с учетом только деформации пружины при Mq = М, определяется уравнением (7.4)

х = Хга - М,,А + МЛ.

Очевидно, дополнительное перемещение k,. диска 3 за счет перемещения опоры пружины будет равно разности

= X - Х = Хт - МхА + МА

(7.11)

По условию принято, что Хт = Ут, кромс ТОГО, В цслях упрощения конструкции рассматриваемого узла желательно, чтобы при Мх = М VL при = Муп величина равнялась нулю, а угол подъема винтовой линии резьбы вала соответствовал бы не более чем одному обороту (в относительном движении) диска при перемещении его вдоль оси на величину Хт - Xq. Здесь Xq -минимальное значение х, при котором крутящий момент М,. равен М-т - максимальному заданному значению.

При этих условиях уравнение (7.11) принимает вид

kxOy+MA-MxA-,

откуда

{Ут + МА) + (Ут-МА) Мх--2А "

ТО есть будет равно нулю при двух значениях М, когда:

1) М = М;

... Л/Г

(7.12)

2) M, = -fi = M,„=i

Формула (7.12) определяет значение А, при котором удовлетворяется поставленное условие:

8гОз

М /-,р tg (у -f- р) Gd* •

(7.13)

При известном А можно найти максимальное значение =„. Для этой цели, взяв производную но уравнению (7.11) и приравняв ее нулю, получаем

dkx М л о

- ,,2 Ут Л -

откуда Мх, при котором = будет равно

Mx=Y-

(7.14)

Подставляя полученное значение М в уравнение (7.11), после преобразований получаем

(7.15) 199»

кгп={УУт-УМЛГ.