ю в 6

Кривые изменения величин х, х, i, и N в зависимости от даны на рис. 157, из которого видно, что мощность N в пределах изменения момента от нуля до номинального Mq возрастает по наклонной прямой, при дальнейшем увеличении

мощность сохраняется постоянной.

В заключение следует заметить, что вариатор, построенный в соответствии с рассматриваемой схемой, не может быть использован для реверсивного движения.

В случае необходимости, реверсивное движение осуществляется при условии, что ведомый диск с валом соединен промежуточным звеном в виде полого цилиндра с разноименной резьбой в отверстии и на наружной поверх-

О 4 8 12 W 20 24 гвМхкгм

Рис. 157. График изменения N, Xi, i. хккх в зависимости от Мх для вариатора с перемещающейся опорой пружины.

ности цилиндра. Характеристика этих резьб должна быть одина-. ковой, т. е.

юр tg (ср, + Pi) = Ггср tg (срз + Рз).

2. ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИКИ ВАРИАТОРА С КАЧАЮЩИМСЯ НА ВОДИЛЕ КОНИЧЕСКИМ ДИСКОМ

Рассматриваемый вариатор скорости, в отличие от лобового, с изменением крутящего момента на ведомом валу автоматически регулирует передаточное отношение независимо от направления вращения ведущего вала.

От конического диска / /.2,

(рис. 158), закрепленного на ведущем валу, движение силами трения передается диску 2. Диск 2 закреплен на валу 3 направляющими щпонками и может перемещаться вдоль оси вала, изменяя при этом длину пружины 6. Зубчатое колесо z, вращаясь вместе с валом 3, передает движение ведомому валу 4 через зубчатое колесо Zg. Вал 3 установлен в подшипниках водила 5 и вместе с ним может качаться относительно оси вала 4, при этом изменяется положение диска 2 относительно оси вала 3 и диска / и соответственно изменяется передаточное отношение вариатора.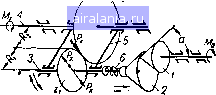

Рис. 158. Схема вариатора с качающимся на водиле коническим диском.

Положение водила 5 зависит как от величины, так и направления крутящего момента Му,, приложенного к ведомому валу 4, так как с изменением момента изменяется давление на зубья колес г, и и составляющая нормального давления между дисками, воспринимаемая пружиной б.

При исследовании характеристики вариатора принимаем следующие допущения: сила трения вдоль образующей конуса в период работы вариатора равна нулю; радиальная составляющая нормального давления между дисками / и 2 (рис. 159, а) при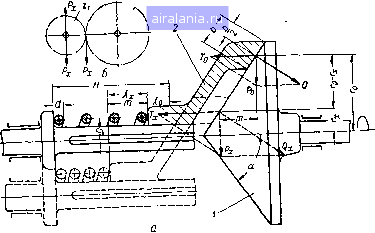

Рис. 159. Схема сил, действующих иа ведомый диск вариатора.

всех возможных положениях водила параллельна окружному усилию Ру зубчатых колес Zj и (рис. 159, б) и равна ему по величине, что соответствует Za = оо.

Тогда угол а образующей конических дисков определяется из условий (рис. 159, а)

Величина силы Р, без учета потерь определяется формулой

р м1 г„ " rxRi •

Передача движения коническими дисками без буксования возможна при условии

QJ = B = , / (7.16)

з: Гх COS а >

где / - коэффициент трения скольжения; - коэффициент надежности; Л1о - крутящий момент на валу ведущего диска;

Го - радиус начальной окружности ведомого диска 2;

- радиус начальной окружности ведущего диска /;

- радиус начальной окружности зубчатого колеса z. Подставляя значение в равенство (7.16), получаем

cos а =

(7.17)

Деформация Xq пружины, соответствующая первоначальному соосному положению дисков 1 и 2 и обеспечивающая передачу номинального крутящего момента Mq на ведущем валу, определяется по известной формуле

h=To- = -tgc А.

Величина Xq будет сохраняться до тех пор, пока Г, не станет больше Го, в дальнейшем деформация пружины будет изменяться по закону

x, = rH = tg«. Л.

Перемещение диска 2 вдоль оси вала в соответствии с рис, 159, а равно

m = - Хо. Подставляя значения Х и Xq, имеем

Из того же рис. 159, а получаем

rx=ro-mtga..

(7.18)

Подставляя в последнее равенство значение т из формулы (7.18), имеем

":tg2a.Л. (7.19)

г. = ra + tg2a•Л-

Общее передаточное отношение вариатора определяется формулой

Rirx

Подставляя значение из уравнения (7.19), получаем

(7.20)

Из условий статики без учета к. п. д. вариатора имеем

Подставляя значение ix из формулы (7.20), получаем М, = Мх МхМ, - Ml .

<2 КгГ Го

(7.21)

Как видно из формулы (7.21), Mq зависит от и изменяется по закону параболы, а положение вершины параболы и расположение ее ветвей зависит от Л. Это значит, что при всех прочих равных условиях и различных Л максимальный коэффициент перегрузки fe двигателя, равный

будет различным.

Взяв производную Мо по М из уравнения (7.21) и приравняв ее нулю, определяем значение М, при котором Мо будет иметь максимальное значение. Затем, подставляя полученное значение Мх в уравнение (7.21), после преобразований получаем

А = [(2k- 1)-2y-k(k-l)] . (7.22)

Уравнение (7.22) определяет характеристику пружины Л по выбранной величине коэффициента перегрузки к.

На рис. 160 даны кривые изменения мощности на ведущем валу вариатора для некоторых значений fe при постоянном числе оборотов двигателя.

В рассматриваемой схеме (рис. 159) радиус Го ведомого диска постоянный, а ведущего переменный. Если же, как показано на рис. 161, постоянным сделать радиус Го ведущего диска, а ведомого Гх - переменным, то при определенных условиях, с учетом принятых допущений, характеристика вариатора будет идеальной [10].

Как и прежде

m = Х - Хо = ТхА - ГоЛ.

В соответствии с рис. 161

ГхГо + mtg а.

Подставляя значение т, получаем

. = Гo + ~tga.Л-tga.Л.

(7.23)

Крутящий момент на ведущем валу определяется из выраже-

Мо =

Подставляя значение из формулы (7.23), имеем м

(7.24)

Из уравнения (7.24) видно, что в общем случае момент Мт ведущем валу не постоянный, а при постоянном числе оборотов

аг 0,7 1.2 1,7 2,2 2.7 3.2 3.7 4.2 4.7 5,2 5,7 6,2 6,7 7,2Мх нгы!

Рис. 160. График изменения Ы\ в зависимости от Мх при различных Km.

двигателя непостоянной будет и его мощность, однако при условии, что

крутящий момент на ведущем валу равен

М\ = Мо = const. (7.25)

Следовательно, мощность на ведущем валу постоянна при изменении от значения = ДО значения = Mf.

Постоянство мощности при изменении в указанных пределах обеспечивается при условии, что характеристика пружины определяется выражением:

(7.26)

а первоначальный прогиб пружины равен

\ - о

(7.27)

Если вследствие износа дисков, неточной сборки или по иным причинам не будет соблюдено только равенство (7.27), то характеристика вариатора будет лишь асимптотически приближаться к идеальной с увеличением полезной нагрузки. Максимальное отклонение будет иметь место на изломе характеристики, т. е. в момент, когда передача перестает работать как фрикционная муф-

Соосное шожение Оисков -И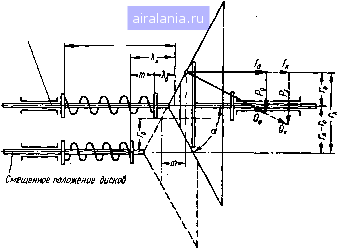

Рис. 161. Схема деформации пружины в зависимости ог перемещения ведомого диска.

та и начинается сдвиг конусных дисков. Относительная величина этого отклонения равна относительной ошибке в затяжке пружины.

В случае невыполнения только равенства (7.26) характеристика вариатора будет идеальной, но не в соответствии с заданной мощностью.

Угол наклона образующей конусных дисков определяется так же, как и в первом случае, по формуле

(7.28)

cosa =

где г,. -радиус ведомого диска. >

Формула (7.28) определяет угол а для каждого значения г, при котором нормальное давление Q. в пределах заданного диапазона равно необходимому. С целью упрощения конструкции конических дисков угол образующей а можно принять постоянным, определяя его при = гр. При этом для всех положений