и определяется только размерами углов ая и ав. Эти углы в су ществующих конструкциях соответствуют участку дуги с наиболее равномерным распределением давления р. Как в первом, так и во втором случаях желательно, чтобы величина силы или регулировалась автоматически в зависимости от крутящего момента на ведомом валу и положения катка..2.

Ниже изложены теоретические исследования для двух случаев: давление между катками осуществляется перемещением катка 2 и перемещением катка /.

Предполагая, что каток /, изготовленный из стали, не деформируется, а деформируется только каток 2, изготовленный из текстолита или других пластических материалов, и что линейное давление прямо пропорционально деформации в направлении нормали, напишем

где р2 - линейное давление в кг/см; е - деформация катка 2 в см; С - коэффициент пропорциональности. Деформация по нормали произвольно выбранной точки (рис. 12,а) определяется равенством

е = 8о cos а,

где \ - перемещение центра Ог в вследствие деформации катка 2;

а - угол, координирующий элементарную дугу контактной линии, ограниченной углом da.

Подставляя значение е в формулу для р, получаем:

P2 = -gCosa; p2« = -gCosaя; р2в= cosub.

Решая полученные равенства относительно и приравнивая их, имеем:

Рг = Р2В;

cos а

(1.37)

Проектируя все силы на направление действия силы Qg, рассмотрим равновесие катка 2

= j dN cos a = P2 J cos ada,

"B

где Рз - радиус кривизны образующей катка 2.

Подставляя в правую часть значение р из формулы (1.37), после интегрирования и преобразования получаем максимальное значение линейного давления в точке В

22 cos ад

Р2в =-;-. (1-38)

Соответственно минимальное давление в точке Я

2Q2 cos a

Р2Я =

("я - "в) + 2" 2°я - sin 2аз

Среднее линейное давление с достаточным приближением принимаем как среднее арифметическое

Р2В + Р2Н 2 (cos Ojg + cos aj)

P2cp =

P2cp = Q2C2,

(1.39)

где с2 - величина постоянная.

По аналогии с изложенным были получены формулы для линейных давлений по контактной линии, когда катки прижимаются усилием посредством перемещения катка / Вдоль оси (рис. 13, а)

„ PiB + P\H Plcp - -я- =

Qi [sin {afj - <f) + sin (ag - (p)]

- "b) + у sin 2 (ag - <p) - sin 2 (a - ,y)

(1.40)

Plcp = QiCi, где - величина переменная.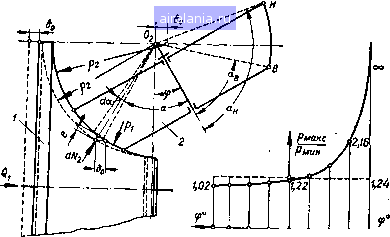

38 30 20 10 0 10 20 30 40 6

Рис. 13. Схема распределения линейных давлений при перемещении катка J и неподвижном катке 2.

Закон изменения отношения максимального линейного давления к минимальному (при = 52" и ад = 40°) для различных положений катка 2 показан на графике рис. 13, б, а закон изменения средних давлений - на рис. 14. Из графиков видно, что более рациональной является конструкция, у которой необходимое давление между катками осуществляется перемещением не катка /, как это имеет место в существующих моделях, а катка 2. На рис. 15 показано два предельных положения катка 2, которые определяются положением оси вращения через углы, ср и ср.

Определим зависимость между cpj и основными параметрами & и Рг катка 2 при рабочей поверхности катка /, ограниченной углом 90°.

Из рис. 15 видно, что

ая = у -9i и ад=ср2, (1.41)

где кя и кв - углы, ограничивающие ширину Ь катка 2.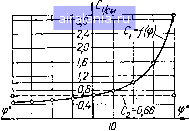

38 30 20 Ю О

20 30 40

Рис. 14. График изменения средних линейных давлений в зависимости от положения катка 2.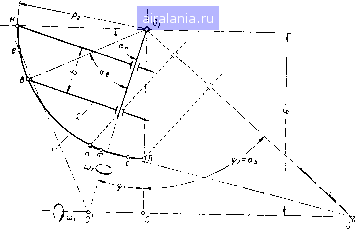

Рис. 15. Схема однополюсного и двухполюсного качения катков. Кроме того,

PgCosKs - р2С05ая = Ь, или cos as - cosa=-, Подставляя значения ад и кя из (1.41), получаем

(1.42)

В большинстве случаев при проектировании вариатора принимают ф2 = fi, тогда

cos - sin срг = V 1 - sin 2ср2 = - ,

откуда

sin2cp2 = sin2cpi = 1 -

(1.43)

Когда вариатор составлен из трёх катков (см. рис. 20),

?1 = Ъ= Y~" ая + ав = у.

Как видно из рис. 15, при угле cpj качение катков без скольжения происходит в одном полюсе е, а при угле .окружные скорости катков могут быть равными в двух полюсах тис.

Определение передаточного отношения вариатора при ведущем катке 1 и ведомом 2

Как и в предыдущих случаях, в рассматриваемой задаче принято допущение, что элементарные силы трения параллельны между собой и перпендикулярны образующей в плоскости чертежа.

Рассмотрим сначала случай чистого качения катков в двух полюсах. Передаточное отношение вариатора (рис. 16)

Ro Ro о г.

Ro = Ра sin с, Ro = р2 sin а., Го = Л - р2 cos (а - ср) и Го = Л - P2C0s(a;„ -ср).

Подставляя значения радиусов в формулу для /i 2, получаем

fl-2 =

Рз sin а.

р, sin а

А - Рз cos («с - ч>) Л - Рз cos (а - щ) •

(1,44)

Неизвестным в формуле (1.44) является угол а. или а, определяющий соответственно пэлюсы качения тис.

Определим углы и а,„ из условия равновесия моментов всех сил, приложенных к катку 2, относительно его оси вращения.

На рис. 16, а показан график разности окружных скоростей 2 и Vi для исследуемого случая. Штриховой линией ограничены концы векторов скоростей катка 2 и сплошной - концы векторов скоростей t»i катка

В соответствии с графиком на участке cm силы трения, возникающие вследствие скольжения и приложенные к катку 2, направлены в сторону, противоположную направлению его вращения, а на участках Вс и тН - в направлении вращения.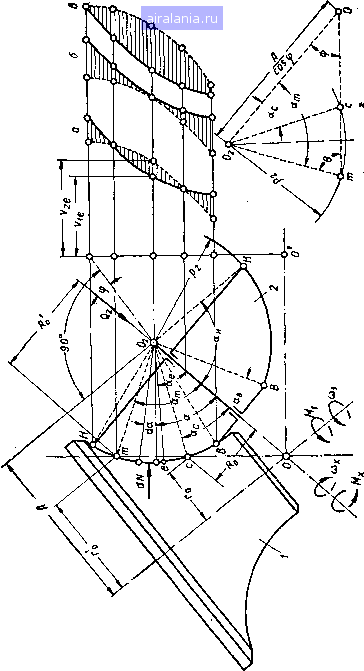

я о.

Е я о

i£

§

Сумма моментов внешних сил и сил трения, действующих на каток 2 относительно оси 00, запишется так:

-М,-Мтс + Мсв + М„„ = 0, (1.45)

где Мх - момент внешних сил;

Мтс - момент сил трения на участке дуги тс;

Мсв - момент сил трения на участке дуги сВ;

Мтн - момент сил трения на участке дуги тН. На любом участке дуги контактной линии, ограниченной углом da, элементарный момент сил трения равен

dM = dNfpsina, (1.46)

где dA/- нормальное давление, приложенное как равнодействующая линейных давлений к рассматриваемому элементу дуги;

Ра -радиус кривизны образующей катка 2; а - угол, координирующий рассматриваемый элемент дуги. Нормальное давление dN определяем по среднему линейному давлению

dN = РгсрРаа.

Подставляя значение dN в формулу (1.46) и интегрируя в пределах рассматриваемых дуг, имеем

Мсв= РаРгср/ (cos ав - cos а)

Мс = РгРгср/ (cos а, - cos а.) . (1.47)

М/пя = рР2ср/ (cos а„ - cos Кя)

После подстановки полученных значений моментов в формулу (1.45) и простых преобразований получаем

Мх = рр2ср/ (2 cos - 2 cos + cos кв - с os ан). (1.48)

Решая равенство (1.48) относительно (cosa - cosa„) и подставляя значение pfcp по формуле (1.39), имеем

cos а.с - cos =

= у jcos ав - cos ая -

(а„ - «в) + у (sin - sin 2яз)

P2Q2/ (cosag + СОЗЯ,)

.(1.49)

* При подстановке действительного значения Рг по формуле (1-37) формула (1.49) имеет вид

1 / 4M..cosan\

cos о. - cos = - соз2ян - cos 2я„ -

т - л \---~в -«я „ 2,

Последующие преобразования этой формулы приводят к громоздким уравнениям четвертой степени. Точность результатов, получаемых по средним линейным давлениям, достаточна для практического применения.