Обозначим

cos а-с - cos а.т = В.

(1.50)

Для решения уравнения (1.50) определим геометрическую зависимость между углами и из треугольника OmOj (рис 16, г). По теореме синусов

- (1.51)

где 6 = 90° - (-

cos sin I

sin ip

ф = 90° -

сро = 2ic + f - угол, определяюш,ий положение катка 2. Подставляя значения 6 и ф в равенство (1.51), имеем после преобразований

i„ "m Л - Р2 cos уо

т - ""7 ~

tg "9 + Р2 cos Ч)„)

(1.52)

Подставляя в уравнение (1.52) значения

о. Г\ - COS а

т-/

1 4- cos

1 - cos 1 + COS a

И решая его относительно cos а, получаем

cos am =

2Лр2 COS tpo - л* COS Ct - P2 COS* tpo COS

Л= + pgcos

• 2Лр2 COS fo COS

(1.53)

Полученное значение cosxm подставляем в формулу (1.50) и, обозначая А/р = К, после преобразований получаем

cos «с = Y

\COS сро

COS сро

+ S -

\cos 9(, к

Таким же путем получаем

coscp„ \2 / ВК , Bcosyo

+ n+2cosf„ +

(1.54)

cos а™ =

2 cos

j COS tpo

, cosyo \ /. ВК Bcoscp„ coso"*" к I \ 2costf(,

2К I

(1.55)

Анализ графика (рис. 16, с) разности скоростей катков показывает, что скорости скольжения могут быть и однозначными (рис. 16, б), что соответствует граничному положению, при котором происходит буксование вследствие недостаточной силы нажат

Тия Q2 или вследствие увеличения момента Мх внешних сил до предельного. В этом случае а = *«мин соответственно

COSOtc - cos Km = 0.

Решая уравнение (1.49) относительно при «„3 = ""мин и обозначая силу нажатия, при которой cos - cos = О, через 2„нн необходимую силу нажатия - через = Q2„„hP, получаем

О, = Оо 3 =

Ра/ (COS ctg -COS af)

(1.56)

где p - коэффициент надежности, который рекомендуется принимать равным 1,15-1,2. Теперь исследуем работу вариатора, когда общая образующая начальных конусов пересекается с образующей катков не в двух, а в одном полюсе. Рассматриваемый случай соответствует условию, при котором полюс с уходит за пределы точки В или полюс т уходит за пределы точки Н. Полагая соответственно для каждого условия Кс = кв и ост = кя И обозначая точку пересечения образующей начальных конусов с образующей катков буквой е, из формулы (1.49) получаем

±

cos = Y COS Kb 4- COS ая ± - в) + у (sin 2с(я - sin 2а)

P2Q2/ (cos ад + cos Ct/)

(1.57)

Знак плюс относится к случаю, когда = ав, и минус - когда

Необходимую силу нажатия катков для случая однополюсного качения можно определить по формуле (1.57), полагая, что начальный момент буксования имеет место при = ав или = кя (рис. 16, в). В результате решения этой задачи получим формулу (1.56).

Важным в рассматриваемой задаче является определение угла сртс. в пределах которого происходит качение катков в двух полюсах. В общем случае переход от двухполюсного к однополюсному качению катков может быть при двух значениях zic-при повороте оси вращения катка 2 влево или вправо от вертикали. Кроме того, в каждом из этих положений оси катка 2 возможны два случая: за пределы контактной линии перемещается полюс с или полюс т. Это зависит от межосевого расстояния А и углов ав, «я и ср.

В первом случае предельное положение определяется совмещением полюса с с точкой В, во втором - совмещением полюса гц с точкой Я.

Решая уравнение (1.54) относительно сро при ас=ав, получаем, значение <ртс для первого случая

1 -f COS °В~ cos Од

cos ср = К

2 cos - В

/"1 + COS Од - BCOS Од

2 cos ад - в

")-

(1.58)

Соответственно решая уравнение (1.55) при о.т = н, определяем значение сртс для второго случая

1 + cos + В cos a

cos ср;, = к

2 cos а „ + В

1 + cos2 afj + В cos а 2

2 cos + В )

(1.59)

Определение передаточного отношения вариатора при ведущем катке 2 и ведомом 1

Напишем сумму моментов сил, приложенных к ведомому катку / (рис. 17) при ведущем катке 2

- М+Мт,с,-Мс,в-Мцг„ = 0. (1.60)

Элементарный момент сил трения для любого участка дуги касания катков определяется по формуле

dM = dNfrx. (1.61)

Как и прежде,

dN = РзРгсра. Плечо силы трения Гх определяется равенством

Гх = Л -p2Cos(a -сро), (1.62)

где сро = 2ic + ср.

Подставляя значения dN и Гх п формулу (1.61) и заменяя cos (а - сро) = cos а cos ср -f- sin а sin сро, получаем

= da -pacoscpj j cosada -pgsincfoj sin ada. (1.63)

P2P2

Интегрируя правую часть равенства (1.63) в пределах дуг qS, ст, тН, соответственно получаем:

Мсв = Р2Р2СР/ [(=1с, - ав) - pgcoscpo (sin а,, - sin 0.3) +

+ P2sincpo(cosa,, - cosas)]; (1.64)

m,c,= PiPzcpf [A {a.m, - - P2cos cp (sin a.,„ - sin acj.+

+ p2sincpo(cosa„, - cosa.J]; (1.65)

ят, = р2Р2ср/ [A (ая - aJ - p2 cos cpo (sin a„ - sin a„J +

+ P2sincpo(cosa«-cosaJ]. (1.66)

Подставляя значения Мс,в, Mm.c,, Мят, и рср из формулы (1.39) в сумму моментов (1.60), после преобразований получаем

(«т. - «с.) - (sin am, - sin а,,) - tg сро (cos а,, -- cos am.)

P2 cos (po

" Pa cos (po

(ая - ав) - (sin ая- sin ад) - tg cp (cos ав - cos a«) +

("я - "в) + у (sin 2a - sin 2ag)

P2Q2/ (cos + cos a,) cos <po

(1.67)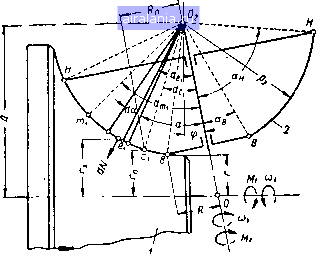

Рис. 17. Схема скольжения по линии контакта при ведущем катке 2 и ведомом /.

Уравнение (1.67) решается табличным способом. Для этой цели следует задаться рядом значений а,, и по формуле (1.52) определить соответствующие им а,.

Результаты действий, произведенных для левой части уравнения по каждому значению а,, и а, сравнивают с правой частью, которая для данного значения ср = 2ic ± ср является величиной постоянной.

Подставляя в формулу (1.67) предельные значения углов а== = ая и а, = ав, соответствующие условию, граничащему с буксованием, получаем

(ая - ав) - (sin ая - sin ав) - tg сро (cos ав - cos ад) =

Ра cos (ро

("я - "в) + у Я - sin 2с(д)

P2Q2/ (cos ад + cos afj) cos <fo

(1.68) 35

Обозначая левую часть равенства (1.68) через D, определим необходимую силу нажатия

(я ~в) + -2 (sin - sin 2ag)

(1.69)

Лрз/ (COS (2д + cos ct) cos

Выше был рассмотрен случай пересечения образующей начальных конусов с образующей катков в двух полюсах. Пересечение образующих в одном полюсе соответствует двум условиям:

а-с, = о-в при а = а

«т, = «Я при а-с = ае,

где б; - полюс качения.

Подставляя эти условия в формулу (1.67), соответственно

получаем

2 (о7„ " - " + =Ро cos а,, ) =

Р2 COS (f„

(«Я - as) - (sin ад -]- sin ая) + tg ср (cos а -f cos ая) ±

(«я -в)+-2 (sin 2с<я - sin 2а)

P2Q2/ (cos cig + COS ctj) cos t

(1.70)

Рассматривая предельное значение угла а, граничащее с моментом буксования, когда а,. = ав или а = ая, получаем формулу (1.69), определяющую необходимую силу нажатия катков.

Уравнение (1.70), как и уравнение (1.67), решается табличным способом.

Передаточное отношение вариатора при ведущем катке 2 и ведомом / определяется отношением (рис. 17). при двухполюсном качении катков

Га Л - Рз cos (а -у) л - Ра cos (а - ср)

Ч-1 - - -

(1-71)

(1.72)

0 p2Sina PzSina

И при однополюсном качении

л - р2 COS (а,-ср) pasma

Заканчивая исследования кинематики вариатора, следует отметить, что наименьшее скольжение, а следовательно, и наименьший износ катков имеют место при двухполюсном качении. Соотношение между Л и ср при двухполюсном качении катков определяется формулой (1.52), приведенной к виду

А = P2C0S сро

P2COS сро

(1.73)

Полагая, что

а = а, =

«я + «в

получаем приближенно

1 +tg

Л Р2 cos сро-

/"Я + B

= Р2

COS с

H Т- В

(1.74)

Предельные значения углов ср, при которых качение одновременно происходит в двух полюсах, определяется по формулам (1.58) и (1.59).

Определение коэффициента полезного действия вариатора

Не останавливаясь на общеизвестных методах определения полного к. п. д. механизма, определим к. п. д. вариатора с учетом только потерь, возникающих вследствие геометрического скольжения катков в зоне контактной линии.

Прежде всего рассмотрим случай, когда каток / - ведущий, а каток 2 - ведомый, качение катков происходит без скольжения в двух полюсах.

В качестве исходного выражения, определяющего к. п. д. вариатора, принимаем известную формулу

- = Mfc (•>

где - крутящий момент на ведомом валу вариатора в кг-см; All - крутящий момент на ведущем валу в кг-см; z\ 2 - передаточное отношение.

Крутящий момент на валу катка /, когда он является ведущим (см. рис. 16), определяется по формуле

М-Мн-Мвс + М,„,0.

(1.76)

Подставляя в формулу (1.75) значения по формуле (1.48), ii 2 по формуле (1.44), Мц по формуле (1.66), Мвс по формуле (1.64) и М,пс по формуле (1.65), после ряда преобразований получаем

Л - р2 cos(a - ср)

"1-2=-

р2 sin ас

- (2a-2ayn+afj-ag) -cos ср„(2 sin а-2 sin a„j+sin а - sin а)

2 cos о.уп - 2 cos а + cos ag - cos a

- sin cpo

, (1.77)

где ao = a.

Предполагая, что в формуле (1.77) а = а.н при а = а или о-с = ав при о. = ае, а также кдк в одном, так и в другом слу-