чаях dc = de, получаем формулу, определяющую к. п. д. вариатора при однополюсном ка.чении катков

А - Рг cos (ае - Ч>)

1-2=-

- (2ае -a -а) - cos еро (2 sin ае - sin - sin а)

-----sin фо

cos «я + cos - 2 cos

(1.78)

В случаях передачи движения от катка 2 к катку / исходное уравнение для определения к. п. д. вариатора имеет вид

(1.79)

При двухполюсном качении катков момент М, определяется из формулы (1.67) в соответствии с формулой (1.39):

1 = /Р2р2ср [А (2а„, - 2а,, + ав - ая) -

- Ра COS ср„ (2 sin а„, - 2 sin а,, + sin ав - sin ая) - (1.80)

- Ра sin сро (2 cos а,, - 2 cos а, + cos ая - cos ав)].

Сумма моментов всех сил относительно оси вращения ведущего катка 2 (рис. 17) запишется так:

М + М„ + Мвс - М,„ = 0. (1.81)

Подставляя в формулу (1.81) значения моментов Мя, Мвс, Мс„ по формуле (1.47), имеем

к = РгРгср/(2 cos а,, - 2 cos аш, + cos ая - cos ав). (1.82)

Подставляя в формулу (1.79) значения М, по формуле (1.80), по формуле (1.82) и ia-i по формуле (1.71), после преобразований получаем

2-1 =

- (2ат,-2ас,+ав-- cos 9,, (2 sin sin a-f sin a-sin a)

2 cos a, - 2 cos ctm, + COS - cos Ojc

- Sin cpo

P2 smote,

Л-рз cos где a,, = a,..

В случае пересечения образующей начальных конусов с образующей катков в одном полюсе по тем же условиям, что и при выводе формулы (1.78), получаем

2-1 =

- («я + «в - 2а,) - cos tpo (sin a + sin - 2 sin a)

2 cos a„ - COS ct D - cos (

- sincpo

Рг sin oe,

. /1 - P2 cos ("e-To)

(1.84)

В частном случае (рис. 18) при ведущем стальном катке /, ведомом 2 из текстолита, постоянном = 150 кг-см, / = 0,2, р= 1,2, р2= 100 мм, Л= 142 мм получены следующие результаты: О, = 90 кг; ров = 66 кг/см; ср = + 39°; ав = 39°; ая = 51°; й= 15 мм; ср;, = 25° 1320"; а, = 50°730"; а,„-ае;1°; h a = = 0,546-f-1,748 и -rii a = 0,995-0,931 (рис. 19).

ае=50°7 30

В пределах 2f положений,.

(±р„1.=25°1320") дЬухпотсное

качение В остальных положениях однополюсное качение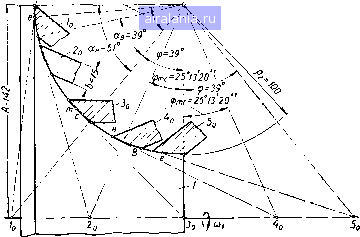

Рис. 18. Схема вариатора с однополюсным и двухполюсным качением катков.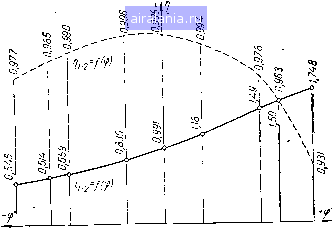

39 30 25 Однополюсное, I качение I

ддухполюсное качение

25 30 39

пднополюснов. качение

Рис. 19. График изменения к. п. д. и передаточного отношения вариатора в зависимости от положения катка 2.

Вариатор скорости, составленный из трех катков ,

В машиностроении наиболее широкое применение получили вариаторы, составленные не из двух, а из трех катков (рис. 20). Каток / является ведущим, 3 - ведомым или наоборот. Каток 2 является промежуточным и служит для изменения передаточного отношения. Результаты теоретических исследований, изложенные выше, применимы и для данного вариатора, если последовательно рассматривать катки 1 и 2 при ведущем / и затем катки 2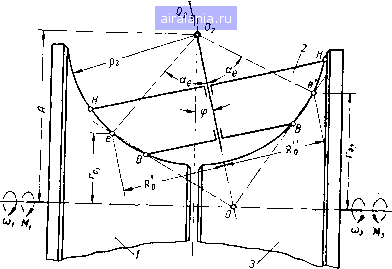

Рис. 20. Схема вариатора скорости с промежуточным диском.

и 3 при ведомом 3. При этом следует учесть, что сила Q, прижимающая каток 2, в данном случае воспринимается не одним, а двумя катками [1 и 5). Следовательно, в знаменатель формулы (1.39), определяющей среднее линейное давление, необходимо ввести двойку

, (?2 (созад + cosa,)

Р2ср -

{"Н - "в) (S" - sin 2aj)

(1.85)

Соответствующие изменения следует внести также во все формулы, в которые входит значение рср-

Общее передаточное отношение г, з вариатора, составленного из трех катков, определяется произведением г\ 2/2 з. например, при однополюсном качении катков

. А - Р2 COS (а + у) h-3-tl-h-3~ Л-р2СОЗ(ос, + у) •

(1.86)

Верхние знаки соответствуют отклонению оси ролика 2 вправо от вертикали, а нижние - влево.

Коэффициент полезного действия вариатора

Коэффициент скольжения рассматриваемого вариатора скорости олределяется по формуле

= + (1-88)

0,33 0,4 0,3 0,66 1,0 1,5 2,0 2,5 3,0

Рис. 21, График изменения коэффициента скольжения хорового

вариатора.

Пренебрегая произведением ejSj, можно с достаточной для практических целей точностью определить

г = + £2,

(1.89)

где £j - коэффициент скольжения для контакта катков / и 2 при ведущем катке 1:

£ = 1

1-2

и S2 - коэффициент скольжения для контакта катков 2 я 3 при

ведущем катке 2:

32=1-

Передаточные отношения i[ 2 и /з-з определяются по средним радиусам, а действительные передаточные отношения г\ 2 и /2-3 - с учетом скольжения по контактной площадке.

На рис. 21 дан график изменения коэффициента скольжения е в зависимости от передаточного отношения для вариатора, выполненного по схеме торового вариатора [27].

В заключение следует отметить, что рассматриваемый вариатор при сопоставлении его с другими схемами имеет наименьшее значение е.

в начальный момент в точке,

3. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ, КОЭФФИЦИЕНТА СКОЛЬЖЕНИЯ И К. П. Д. ВАРИАТОРОВ, РАБОТАЮЩИХ С НАЧАЛЬНЫМ КОНТАКТОМ В ТОЧКЕ

Известно, что в общем случае тела качения, соприкасающиеся

под действием нормальных сил деформируются и контакт в точке переходит в контакт по некоторой площадке, имеющей эллиптическую форму (рис. 22, а). Скорости колес вариатора в различных точках контакта будут различными, и .только в одной из них (точке О) которая не совпадает с цент ром О площадки (рис. 22, б) окажутся одинаковыми. Распо ложение точки О зависит от рас положения осей валов фрик ционных колес и взаимного расположения вершин образующих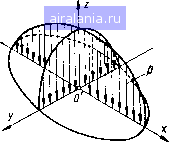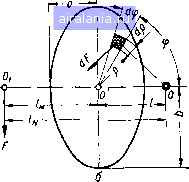

(iF=fppcipa(p

Рис. 22. Схема расположения полюсов качения при начальном контакте фрикционных катков в точке.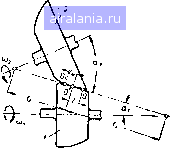

Рис. 23. Схема вариатора с начальным контактом в точке.

конусов по касательной к площадке контакта (рис. 23). В частном случае, когда оси валов расположены в одной плоскости, точка О (см. рис. 22, б), в которой скорости одинаковы, и точка Oj приложения равнодействующей сил трения F расположены на линии малой полуоси эллипса, а расстояния / и от центра площадки для данного передаточного отношения зависят только от коэффициента надежности д,,

Р~Т- Мх •

Потерн, возникающие вследствие скольжения между площадками контакта, очевидно, будут тем меньше, чем меньше расстояние In между точками О и О.

Построив график геометрического места точек О и Oj в зависимости от р (рис. 24), можно установить оптимальное значение коэффициента надежности, при котором потери на скольжение будут минимальными. По графику оптимальное значение 3 находится в пределах от 1,25 до 1,67.

Величина скорости скольжения для точки касания О (см. рис. 23) определяется так:

h-2а-

ДОО = [V0-]i - [V0]2,

[vo-]i = coi/i sin ttj

[vo]2 = h2 sin a-

Подставляя значения скорости [vo], точки О катка 1 и скорости [оо], точки О катка 2 в формулу для Дуо-, получаем

Avo = u)i/i sin aj - coj/asin a. Заменяя

(0„ = (0

(/i - I) sin cti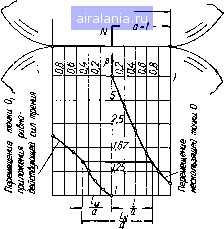

1 (/2 + I) sin ОС,

после преобразований имеем

Рис. 24. График геометрического места точек О и 0,1 в зависимости от р.

ДУо-= coi/Sinai 1+

к ± i

(1.90)

Соответственно скорость скольжения для точки приложения равнодействующей сил трения f (точки 0) определяется формулой

(/i + /2)

ДУо, = oil sin al

(/2 ± I)

(1.91)

Коэффициент скольжения s для рассматриваемого случая определяется формулой

(1.92)

s= l--i-

где / - передаточное отношение вариатора, определяемое по средним радиусам: i = 4 ;

ll sin OCj

ig - передаточное отношение вариатора, определяемое по радиусам, соответствующим нескользящей точке О: /g=- ±1 "а Подставляя значения i и ig в (1.92), определяем

(k-Osinai-

е= l--ifci). h (/2 ± /)

(1.93)