

|
|
Главная -> Радиочастотные линии 0 1 2 3 4 5 6 7 8 9 [10] 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 Из анализа ф-лы (2.67) следует далее, что от рл:=я/2 т рх=п или от л:=А/4 до х=1/2 сопротивление Zo меняется от минус бесконечности до нуля, так как tgpx меняется от минус бес- 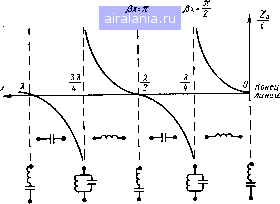 Рис. 2.4. Зависимость, входного сопротивления короткозамкнутой лини» без потерь от ее длины. конечности до нуля. При этом сопротивление линии имеет емкостный характер. При малых значениях р/ входное сопротивление линии можно считать равным Zo = -iZ,tgpZ»-iZ,p/. (2.69) Модуль этой величины можно рассматривать как емкостное сопротивление, равное 1/соС.эь-в. Величина Сяив будет емкостью конденсатора, эквивалентного по своему сопротивлению данной короткозамкнутой линии. Далее на участке линии от х=к12 до л: = Зл/4 линия снова ведет себя как индуктивное сопротивление и т. д. Таким образом, короткозамкнутая линия представляет собой индуктивное сопротивление от х = 0 до х=Я/4, от х=к/2 до X = 3 1/4 и т. д. и емкостное соиротивление от х = к/А jxo х = kl2, от А- = Зл/4 до л- = А и т. д. Прн х = 0, х=к12, х = к и т. д. входное сопротивление равно нулю и линию можно рассматривать как резонансный контур из последовательно соединенных индуктивности и емкости (см. рис. 2.4). При х=к/4, х=Зк/4 и т. д, входное сопротивление равно бесконечности и короткозамкнутую линию можно рассматривать как параллельно соединенные индуктивность и емкость. Проведенный анализ показывает, что с помощью коротко-замкнутого отрезка линии без потерь или с пренебрежимо малыми потерями при заданной частоте можно воспроизвести любое заданное реактивное сопротивление. При этом длину отрезка следует выбирать равной • arc tg При учете имеющихся в линии потерь входное сопротивление короткозамкнутой линии необходимо рассчитывать по ф-ле (2.52): Zo = Zthyx = Zg th (ал; -f i f,x). В этом случае в точках линии, соответствующих минимуму напряжения и тока, можно получить следующие выражения входного сопротивления: ZMHH=Zsth axZax, ZucZcthaxZ- , где л; - расстояние от конца линии до соответствующего минимума напряжения или тока. Определим входное сопротивление четвертьволновой {х-=к/4) линии, но без пренебрежения ее затуханием. Воспользуемся также ф-лой (2.52). При этом будем полагать, что волновое сопротивление является чисто активным и равно Z=\/~LfC, где L и С- соответственно индуктивность и емкость на единицу длины линии. Имея в виду, что i\iyX = Va{ax+\f>x)= h«xcospr-f i charsinpr ch a л-cos p jr-f i sh a jt sin p л-И что при длине линии, равной Л,/4, получим. 1Ьул:= 1/th ах. Так как аргумент ах мал, то 1Ьал:«ал: и thулгл l/ax Подставив это значение в ф-лу (2.52), получим Zo = Zjax. (2J1) Имея в виду ф-лу (2.23), в которой можно пренебречь вторым членом и положить, что а = RI2Z, (2.72) где R - активное сопротивление линии на единицу длины, и что x-kjA, получим ZoSZllRk. (2.73) По этой формуле можно рассчитывать входное сопротивление короткозамкнутой четвертьволновой линии. Следует отметить, что такое же сопротивление будет иметь линия и при л;=ЗЛ,/4 5 Я/4 и т. д. При разомкнутой линии или, как принято называть, в режиме холостого хода ток на конце h будет равен нулю. Выражения для Рис. 2.5. Разомкнутая линия без потерь тока и напряжения в точке на расстоянии х от конца (рис. 2.5) на основании ур-ний (2.38) и (2.39) можно записать: Ох = Ui cos р X, Д = i4sinBA:. (2.74) (2.75) Полагая, что напряжение в конце линии меняется по синусоидальному закону, можно написать следующие формулы, выражающие мгновенные значения тока ix и напряжения Ux на расстоянии X от конца линии: "ж = и,т COS р л: sin СО t, (2.76) = ЧМ sin рл:sin (со+ я/2). (2.77) 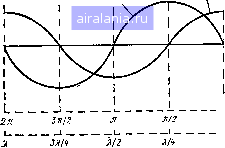 Эти формулы показывают, что при разомкнутой линии имеют место стоячие волны (амплитуда зависит от точки на линии, тогда как фаза во всех точках ли-uJZgsinjix. Ц,щСО!Лх НИИ одинакова), потерь в линии нет (напряжение и ток сдвинуты по фазе на 99°). Сравнивая ур-ния (2.76) и (2.77) с ф-лами (2.65) и (2.66) для короткозамкнутой линии, можно видеть, что закон изменения напря-жения в ней отвечает зако-D ну распределения тока в разомкнутой линии и наоборот. Рис. 2.6. Изменение амплитудны.х значений Закон изменения напря-тока и напряжения в разомкнутой линии жения И тока в разомкну-без потерь . ЛИНИИ показан на рис. 2.6. В этом случае пучности напряжения и узлы тока соответствуют точкам линии, в которых д: = О, Я/2, Я и т д. Узлы напряжения и пучности тока соответствуют точкам линии, в которых х = Я/4, ЗЯ/4 и т. д. Входное сопротивление разомкнутой линии без потерь в точке X (см. рис. 2.5) в направлении к ее концу может быть определено как отношение напряжения к току в точке х линии. Из ур-ний (2.74) и (2.75) получаем = = iJjix = - i ctg р X. (2.78) Отсюда следует, что входное сопротивление разомкнутой линии без потерь, так же как короткозамкнутой, является чисто мнимой величиной и зависит от волнового сопротивления, длины линии и частоты тока. График зависимости входного сопротивления от длины линии показан на рис. 2.7. Здесь явления носят обратный характер по сравнению с короткозамкнутой линией. В этом случае при изменении длины линии от д: = О до л: = 1Я/4, т х = Я/2 до л:=:ЗЯ/4 и т. д. линия ведет себя как емкостное сопротивление; от л:=Я/4 до лг=Я/2, от лг=ЗЯ/4 до х=К и т. д. - как индуктивное сопротивление. При x=0, Я/2, Я и т. д. линию можно рассматри- О конец, тии Рис. 2.7. Зависимость входного сопротивления разомкнутой линии без потерь от ее длины 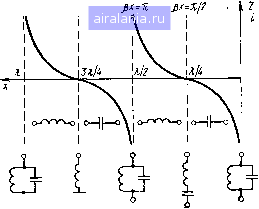 вать как параллельный резонансный контур, сопротивление которого равно бесконечности; при х=Я/4, ЗЯ/4 и т. д. сопротивление линии равно нулю, и она может быть уподоблена последовательному резонансному контуру. При учете имеющихся в линии потерь входное сопротивление разомкнутой линии необходимо рассчитывать по ф-ле (2.53) =Z3cth (ctx-f ipx). В случае разомкнутой линии с потерями в точках, соответствующих л;=Я/4, ЗЯ/4, 5Я/4, входное сопротивление не будет равно нулю, а при л;=Я/2, Я и т. д. не будет равно бесконечности, а будет соответственно иметь минимальные и максимальные значения, определяемые по формулам: Z,px, » Zja. X. Определим входное сопротивление четвертьволновой разомкнутой линии, обладающей потерями. При этом будем полагать, что волновое сопротивление является чисто активным, т. е. ZbV L/C. Имея в виду, что ch к дг cos р х -- i sh к jr sin р jf cth V X = cth (а л: -f i р х) = и что при длине линии, равной sh а л- cos р л; -- i ch а jr sin р X Я/4, cos рх -cos~=0, (2.79) sin px=3 = sin-=1, получим cth YX=thax» ax. 3-320 Подставив это значение в ф-лу (2.53), получим Используя ф-лу (2.72) при х=.К14, получаем 2„ = Я/?/8. (2.80) (2.81) По этой формуле можно определять входное сопротивление разомкнутой четвертьволновой линии, имеющей активное сопротивление, равное R. 2.6. ЛИНИЯ БЕЗ ПОТЕРЬ, НАГРУЖЕННАЯ НА РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ Рассмотрим случай, когда линия без потерь нагружена на чисто реактивное сопротивление (т. е. индуктивностью L или емкостью С, рис. 2.8). Имея в виду, что нагрузка линии Zi = ±iXi Рис. 2.8. Линия без потерь, нагруженная на реактивную «агрузку (знак «плюс» соответствует индуктивности, знак «минус» - емкости), а Ui=IiXi, напряжение и ток в точке линии, расположенной на расстоянии х от ее конца, в соответствии с ур-ниями (2 38) и (2.39) будут = i /, (Zb sin Р д: ± X, cos р х), (2.82) (2.83) 4 = /;/cospA:±sinpA:) . \ Zg у Преобразуем эти уравнения следующим образом: / Z„ . „ . Xi , V в + ? sinpri Введем обозначения: = созрдго. COS р л: ± ; cos р л; sinp; Xi . о -- = sin Р Xq. Тогда выражения, стоящие в скобках, будут представлять собой соответственно синус и косинус суммы двух углов, а ур-ния (2.82) и (2.83) можно будет записать так: = hmY4 + ? sinp (д:± Хо) е cos р (л: ± Xf,) е (2.84) (2.85) Полагая, что ток в конце линии Il=lnQ, т. е. меняется по синусоидальному закону, для мгновенных значений получим и, = /Z2 -f X] sin р {X ± Хо) sin (со / -f 2 cos (л: ± лгд) sin at. (2.86) (2.87) Сравнивая эти выражения с ф-лами (2.65) и (2.66) для короткозамкнутой линии без потерь, видим, что они аналогичны. Разница состоит лишь в том, что аргументы синуса и косинуса амплитудных значений имеют сдвиг на величину ±Хо. При этом знак «плюс» соответствует индуктивной нагрузке, а знак «минус» - емкостной. Уравнения (2.8 и (2.87) показывают, что амплитуды напряжения Yl + X, sinp(xdzxo) и тока COS Р (X ± ЛГо) находятся в зависимости от координа- ты X и фазы напряжения и тока постоянны. Это - характерные признаки стоячей волны. Следовательно, в линии без потерь, нагруженной на чисто реактивное сопротивление, существует только стоячая волна. Амплитуда отраженной волны будет равна амплитуде падающей волны, что означает полное отражение электромагнитной энергии от реактивной нагрузки. Фаза же отраженной волны будет зависеть от величины и знака реактивного сопротивления нагрузки. Рис. 2.9. Изменение амплитудных значений тока и напряжения в линяя без потерь прн индуктивней нагрузке 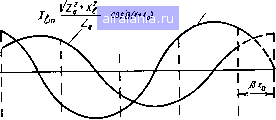
0 1 2 3 4 5 6 7 8 9 [10] 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 0.0092 | |||||||||||||||||||||||||||||||||||