На рис. 2.9 и 2.10 показаны кривые изменения амплитуд напряжения и тока в зависимости от расстояния от конца линии соответственно для индуктивной и емкостной нагрузок. Из этих рисунков видно, что для получения распределения амплитуд, ана-

{т }/zfKl SinJS(X-X„)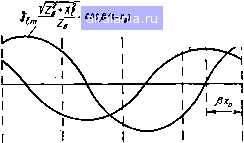

Рис. 2.10. Из.менение амплитудных значений тока и напряжения в линии без потерь при емкостной нагрузке

логичного короткозамкнутой линии, в случае индуктивной нагрузки необходимо добавить к ее длине величину Ха, а в случае емкостной нагрузки укоротить на величину х.

Для определения входного сопротивления воспользуемся ур-ниями (2.84) и (2.85). При индуктивной нагрузке получим

2вх = UJli = \1вЩ{х + Хо). (2.88)

Из сравнения выражений (2.67) и (2.88) видно, что линию без потерь, нагруженную индуктивным сопротивлением X; = ico/, можно заменить короткозамкнутой линией, удлиненной на величину Хо (рис. 2.11). Короткозамкнутый отрезок линии без потерь длиной Хо должен иметь входное сопротивление coL. Величину Хо можно определить из выражения Zstg рхо = &L. При емкостной нагрузке, когда Xi = i/u) С,

2вх = 12в1ёр(х-Хо). (2.89)

Из этого уравнения видно, что линия без потерь при емкостной нагрузке эквивалентна также короткозамкнутой линии, укороченной на величину Хо. Величина Хо может быть определена из выражения tg (-рхо) = I/ZbwC.

Вместо укорачивания линии при емкостной чисто реактивной нагрузке ее можно было удлинить отрезком Xi разомкнутой линии (рис. 2.12), по входному сопротивлению равным сопротивлению емкостной нагрузки Xi=-l/co С. При этом величина Xi может быть определена из выражения tg pxi=ZbCo С.

Таким образом, по входному сопротивлению линию без потерь, нагруженную на чисто реактивную нагрузку, можно рассматривать как короткозамкнутую или разомкнутую линию без потерь, удлиненную на соответствующую длину.

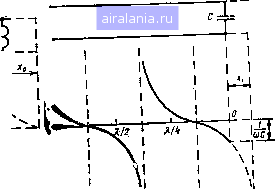Рис. 2.11. Зависимость входного сопро- Рис. 2.12. зависимость входного со-

тивления линии без потерь, нагружен- противления линии без потерь, нагру-

«ой на индуктивное сопротивление, от женной на емкостное сопротивление,

ее длины от ее длины

2.7. ЛИНИЯ БЕЗ ПОТЕРЬ, НАГРУЖЕННАЯ НА АКТИВНОЕ СОПРОТИВЛЕНИЕ

Напряжение и ток в точке, удаленной от конца линии на расстояние X (рис. 2.13), для линии без потерь в соответствии с

Рис. 2.13. Линия без потерь, яагруже»ная на активное сопротивление, равное волновому српротивленпю линии

ур-ниями (2.38) и (2.39) будут равны

[>. = f/cospx-f i/iZeSinpx, 4 = /,cosPx-f i sinx.

Для случая, когда сопротивление нагрузки R равно волновому сопротивлению Zb, можно написать, что Ui~IiZn. Тогда получим = (Ji (cos р X + i sin р X) = еР, (2.90)

4 = /; (cos р X + i sin р х) = /; еР*. (2.91)

Полагая, что напряжение в конце линии меняется по синусоидальному закону, выражения (2.90) и (2.91) можно записать так:

Отсюда мгновенные значения напряжения и тока можно записать в виде уравнений:

«, = [/,sin(co + px), (2.92)

ix = Iim sin {(ut + x).

(2.93)

Из этих выражений видно, что амплитудные значения напряжения и тока во всех точках линии одинаковы, а их фазы зависят от места положения точки на линии. Следовательно, в рассматриваемой линии имеет место бегущая волна, так как эти признаки являются типичными для бегущей волны в линии. В процессе распространения волны напряжение и ток совпадают по фазе.

Из уравнений для и: и ix видно также, что разность в фазах колебания между конечной "Точкой линии и любой, отстоящей от конца линии на расстоянии х, определяется расстоянием между этими точками и скоростью распространения волны вдоль линии. Это можно показать, воспользовавшись, например, ур-нием (2.92):

«а: = /т 51П Ы (t + Х/ш) = U sin О) (/ + Х/Оф),

где Уф = со/р - фазовая скорость распространения волны.

Таким образом, при нагрузке линии на активное сопротивление, равное ее волновому сопротивлению, в линии будут только бегущие волны и энергия будет убывать к концу линии. Этот согласованный режим работы линии является наиболее выгодным режимом работы для передачи активной мощности. Поэтому в линиях передачи применяют специальные меры для получения в них режима бегущей волны.

Входное сопротивление в любой точке линии, нагруженной на активное сопротивление, равное ее волновому сопротивлению, как это видно из ур-ний (2.90) и (2.91), будет равно волновому сопротивлению линии, т. е. Zbx=Zb.

Рассмотрим случай, когда линия без потерь (см. рис. 2.13) замкнута на активное сопротивление R<Zb. Получим для этого случая уравнения передачи. Используя ур-ния (2.38) и (2.39) и имея в виду, что Ui=IiR, для точки х можно написать:

= IlZ [-5- cos рл; + i sin

\ Zg

«X = /,п,2в КБВ sin («< + р jc) + /,„Zb (1 - КБВ) sin р д; X

4 = /, (cos рх + i - sin р X

Введем обозначение

RlZ, = KbB (КБВ<1). (2.94)

При этом далее будет показано, что КБВ является коэффициентом бегущей волны. Можно написать:

t/ =(КБВ cos р л; + i sin р х),

/у. = /, (cos р X + i КБВ sin р х).

Полагая, что Ii=IimeK т. е. ток в нагрузке изменяется по синусоидальному закону, получим следующие выражения для мгновенных значений напряжения и тока: 70

X sinLf+ ,

(2.95)

ix = Am КБВ sin (са / -f р л:) -f (1 - КБВ) cos р д: sin to (2.96)

Анализ этих выражений показывает, что первые слагаемые аналогичны выражениям (2.92) и (2.93) и описывают бегущую волну, а вторые слагаемые аналогичны ф-лам (2.65) и (2.66) для стоячей волны в случае короткозамкнутой линии и отличаются только множителями (1-КБВ). Следовательно, в линии имеются как бегущие, так и стоячие волны; при этом чем больше R отличается от Zb (чем больше КБВ отличается от единицы), тем резче выявлены стоячие волны, и, наоборот, чем ближе КБВ к единице, тем резче проявляют себя бегущие волны. При КБВ = 1, т. е. при R=Zb, в линии будут только бегущие волны (режим согласованной нагрузки), при КБВ = 0 - только стоячие волны (режим короткого замыкания).

Таким образом, коэффициент КБВ характеризует степень приближения режима в линии к режиму бегущей волны и поэтому называется коэффициентом бегущей волны.

Распределение амплитуд напряжения и тока зависит от длины линии. Эта зависимость при значении КБВ = 0,5 показана на рис. 2.14. Из рисунка следует, что при х-0, я, 2я и т. д. ампли-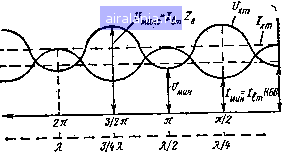

Л X О

Рис. 2.14. Изменение амплитудных значений напряжения и тока в линии без потерь яри нагрузке R<.Z,

туды напряжения минимальны и равны /мин= т2в-КБВ. При рл:=я/2, Зя/2 и т. д., наоборот, амплитуды напряжения максимальны и равны {7макс = Лт2в. Отношение этих амплитуд мин/макс=КБВ равно коэффициенту бегущей волны. Аналогичным путем можно шолучить, что /мин макс = КБВ также равно коэффициенту бегущей волны. В этом случае минимумы амплитуд тока (узлы тока) будут соответствовать максимумам амплитуд напряжения (пучности напряжения) и наоборот.

Входное сопротивление линии, нагруженной на активное сопротивление, меньшее, чем волновое, можно получить, если взять отно"

шение Ux к I. Производя необходимые преобразования, получаем

2вх = 2.

, J 2в (1 - КБВ) sin 2р X

l-(l-KBB2)sin2pA- 2 l-(l-KBB2)sin2pA-

(2.97)

Зависимость активной и реактивной составляющих входного сопротивления от длины линии показана на рис. 2.15. При этом

Рнс. 2.15. Изменение активной (а) и реактивной (б) составляющих входного сопротивления линии без потерь при налрузке RZ

В случае /?>2в аналогичным путем получим следующие выражения для мгновенных значений напряжения и тока:

Ux = КБВ sin {(ut + x) + (К- КБВ) cos р л: sin со t,

(2.100)

=:KBBsin(co/ + PA:) +(1 -КБВ) sinxX

Xsin

H+f).

(2.101)

Первые слагаемые этих уравнений описывают бегущую волну, а вторые - стоячую. Следовательно, в линии имеются как бегущие, так и стоячие волны. При КБВ = 1, т. е. при R=Zb, в линии будут только бегущие волны, при КБВ = 0 -только стоячие волны. Следовательно, КБВ характеризует степень приближения режима в линии к режиму бегущей волны.

Зависимость амплитудных значений напряжения и тока от длины линии при КБВ=0,5 показана на рис. 2.16. Из этого рисуи-

Рис. 2.16. Изменение амплитудных значений на-пряжен1:я п тока в линии бе потерь при наг грузке R>Zb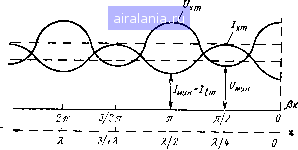

было принято, ЧТО КБВ = 0,5. Данные рисунка показывают, что при х-0, Х/2, Л и т. д. активная составляющая входного сопротивления имеет минимальное значение и равна сопротивлению нагрузки Иь,ши = Я, а реактивная составляющая равна нулю Стело-вательно, . - а

Zbx = /?вх = „ин = Zb КБВ = Z3/KCBH. (2.98)

При значениях x=V4, 31/4 и т. д. входное сопротивление также активно, имеет максимальное значение, но равно

Zb. = /?вх = ?ч,акс = ZR = Z2 ?„„„ = Z/KBB = Z, КСВН,

(2.99)

где КСВН -коэффициент стоячей волны. Во всех других точках линии входное сопротивление имеет комплексный характер. Пр.и этом характер реактивности тот же,, что и у коротко-замкнутой линии.

ка следует, что при px=0, л, 2л и т. д. амплитуды напряжения максимальны н равны [/макс=/т. При рл:=л/2, Зл/2 и т. д., наоборот, амплитуды напряжения минимальны и равны

[/„„„ = ЦКБВ = [/„зкс КБВ. (2.102)

Максимумы и минимумы амплитудных значений тока сдвинуты относительно соответствующих значений напряжения на я/2. При этом

КБВ =

Ulr.

(2.103)

Zb " R Zb КБВ

Из полученных выражений коэффициент бегущей волны равен

КБВ = [/„„„/[/„,„е = /«„„ макс- (2-104)

Сравнивая графики на рис. 2.15 и 2.16, т. е. случаи R>Zb и R<Zb, нетрудно видеть, что они сдвинуты относительно друг друга на я/2 (х = Я/4) и что минимуму в одном случае соответствует максимум в другом и наоборот.