При этом, как видно из ур-ния (2.45), от окружностей Г = const легко перейти к окружностям коэффициента бегущей волны КБВ = = const. Семейство таких окружностей показано на рис. 2.21.

Накладывая друг на друга семейства окружностей rH=const (см. рис. 2.19), д;н= const (см. рис. 2.20) и КБВ = const (см. рис. 2.21), получим диаграмму полных сопротивлений (рис. 2.22).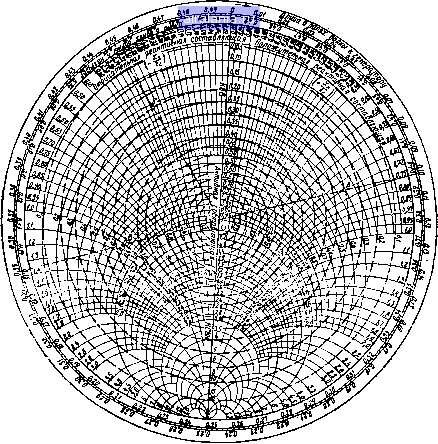

Рис. 2.22. Круговая диаграмма полных сопротивлений

На этой диаграмме масштаб г„ отложен на вертикальной оси. На этой же оси отложены и масштабы КБВ и КСВН, совпадающие с масштабом г. Масштаб Хн нанесен на внутренней стороне обода диаграммы. При этом принято, что г„ и д;„ изменяются от О до 20. Каждой точке плоскости диаграммы соответствуют вполне определенные значения г„, х„ и КБВ, определяемые пересечением соответствующих окружностей и дуг окружностей. 80

Фаза коэффициента отражения нанесена с внешней стороны обода диаграммы и соответствует ее изменению вдоль линии на соответствующую долю длины волны от узла напряжения в сторону генератора (по движению часовой стрелки) или в сторону нагрузки (против движения часовой стрелки).

Диаграмма отражает режим линии на участке, равном половине длины волны. Начало отсчета помещается в узле напряжения, где Гн минимально и отмечено нулем на внешнем ободе диаграммы. Так как распределение напряжений, токов и сопротивлений вдоль линии повторяется с периодичностью через каждые полволны, то целое число полуволн из длины линии исключается. Для удобства работы с диаграммой масштаб КБВ = const (или КСВН = =const или Г=const) целесообразно нанести на прозрачную пластмассовую планку, вращающуюся вокруг центра. При вращении планки риски на ней описывают окружности КБВ = const (или КСВН = const или Г == const).

С помощью круговой диаграммы полных сопротивлений можно решать различные практические задачи. Рассмотрим некоторые из этих задач.

По заданному комплексному сопротивлению нагрузки Zi = Ri+ --1г и заданной длине линии / можно найти входное сопротивление Z-Bx=Risx + i Хв% и коэффициент бегущей или стоячей волны в линии или волноводе.

Допустим, что линия с волновым сопротивлением 75 Ом имеет длину 0,35Я и замкнута на сопротивление Z(= (22,5-f52,5) Ом. Найдем входное сопротивление этой линии. Определим сначала нормированное сопротивление нагрузки: ZBx=ZBx/ZB = rH-f i Хи= = (22,5-i52.5)/75 = 0,3-fi0,7. Затем на диаграмме (см. рис. 2.22) находим точку А, соответствующую /h/Zb = 0,2 и a;h/Zb=0,7. Через точку Л на диаграмме проводим радиус окружности, который на внешнем ободе пройдет через отметку 0,102л. Через эту же точку проходит окружность КСВ.= 5 (КБВ = 0,2). Следовательно, при заданной нагрузке в линии КБВ = 0,2. Активные и реактивные сопротивления линии будут изменяться по длине линии, но все возможные значения будут лежать на окружности КБВ = 0,2.

Нам необходимо найти сопротивление на расстоянии 0,35Я от конца линии. К отметке /=0,102Я, соответствующей концу линии, добавляем 0,35л и получаем 0,452?i. Ставим подвижной указатель на эту отметку и ищем точку пересечения радиуса с окружностью КБВ = 0,2 (точка Б). Эта точка дает значение нормированного входного сопротивления ra+iXu. Из диаграммы получаем Zbx = = 0,23-i 0,292. Отсюда искомое входное сопротивление будет равно Zbx= (0,23-i 0,292)75= 17,2-i 21,9 Ом.

Входное сопротивление линии можно было бы определить и аналитическим способом. Для этого необходимо было бы вести расчеты по сложным ф-лам (2.109).

С помощью круговой диаграммы по измеренному значению КБВ и по положению пучности напряжения на линии или волноводе можно определить величину комплексного сопротивления на-

грузки. Допустим, что на линии с волновым сопротивлением 75 Ом КБВ = 0,35 (установлено при измерениях) и расстояние от конца линии до первого узла напряжения равно 0,15Я. Требуется найти величину сопротивления нагрузки.

На втором ободе диаграммы в сторону, противоположную движению часовой стрелки от нулевого положения (вертикально), находим отметку 1-0,\5к. Соединяем эту точку с центром диаграммы. Ищем точку пересечения полученного радиуса с окружностью КБВ = 0,35 (точка В). Этой точке соответствует нормированное сопротивление Z = 0,8-i0,98. Следовательно, сопротивление нагрузки равно 2г = /?г-ЫХг=(0,8-i0,98)75=(60-i73,5) Ом.

Используя круговую диаграмму, по измеренному значению КБВ и положению пучности напряжения на линии можно определить величину и место включения реактивной проводимости (шунта) для настройки линии или волновода на бегущую волну. При решении такой задачи удобнее оперировать не с диаграммой полных сопротивлений, а с диаграммой полных проводимостей. При этом диаграммой проводимости может служить та же диаграмма сопротивлений, показанная на рис. 2.22. Переход от одной диаграммы к другой весьма прост.

Из выражения (2.108) следует, что между сопротивлениями, разделенными линией длиной Я/4, существует соотношение ZoZx/i =Z\. Деля обе части равенства на Z.\, получаем

(2.130)

или, подставляя нормированные значения сопротивлений, получаем ZaZn =1. На диаграмме сопротивлений четверть волны представляет половину окружности. Поэтому если на одном конце диаметра круга имеем сопротивление Zo, то на другом конце будет сопротивление 1/Zv4 , равное проводимости \jZ(,=yi.

Таким образом, диаграммой полных проводимостей будет та же самая диаграмма, что и диаграмма полных сопротивлений, только начало отсчета будет не в минимуме сопротивлений (минимуме напряжений), а в минимуме проводимости (максимуме напряжений).

Допустим, что из измерений на линии определено положение пучности напряжения и найдено значение КБВ = 0,6. Определим место включения реактивного шунта и его величину для настройки линии на бегущую волну, если ее волновое сопротивление равно 600 Ом.

Окружность КБВ = 0,6 пересекает круг Гн=1 (ё=1) в точке Г (см. рис. 2.22). Соединив эту точку с центром, получим радиус, показывающий, что точка отстоит от пучности напряжения на расстоянии 0,147Я и соответствует проводимости r/i=H-i0,51. Для получения бегущей волны надо в этой точке включить параллельно линии нормированную проводимость, равную -10,51 (индуктивность). Если для настройки целесообразно включить емкость, то надо искать вторую точку пересечения окружности КБВ = 0,6 с

кругом g-l. Эта точка будет отстоять от пучности напряжения на расстоянии 0,353Я (точка Д), и проводимость в ней равна 1/2= = 1-10,51.

Следовательно, в линии будет бегущая волна, если включить нормированную емкостную проводимость -Ы0,51 в точке, отстоящей от пучности напряжения на расстоянии 0,353Я, или нормированную индуктивную проводимость, равную-10,51, на расстоянии 0,147Л.

2.10. РЕЗОНАНСНЫЕ СВОЙСТВА ЛИНИИ БЕЗ ПОТЕРЬ И РЕАЛЬНОЙ ЛИНИИ

Короткозамкнутая линия без потерь имеет входное сопротивление, определяемое выражением (2.67)

Zo = iZtgx = iZtgl,

а разомкнутая линия - выражением (2.78)

Zo„= - iZe ctgA; = - iZeCtgpZ,

где / - длина линии.

Из этих выражений видно, что изменяя аргумент рд: от О до 180°, можно получить любое значение сопротивления от -оо до + СО. при x-XjA входное сопротивление короткозамкнутой линии Zo=oo и линия становится эквивалентной контуру при резонансе токов, а сопротивление разомкнутой линии Zoo = 0 и линия становится эквивалентной контуру при резонансе напряжений.

Короткозамкнутая линия оказывается эквивалентной параллельному резонансному контуру во всех случаях, когда длина линии равна

/ = (2-1)4 {к=\, 2, 3...),

(2.131)

и ведет себя подобно последовательному резонансному контуру, когда ее длина равна

1 = к {к=\,2, 3...).

(2.132)

Для разомкнутой линии эти соотношения меняются на обратные.

Следовательно, отрезки короткозамкнутой или разомкнутой линии могут заменить собой катушку индуктивности, конденсатор или колебательный контур. Опыт показывает, что добротность элементов, состоящих из отрезков линий, можно получить в несколько сотен и даже в несколько тысяч. В то же время добротность контуров, состоящих из сосредоточенных постоянных, при высоких частотах не превышает обычно 100.

Реальная линия передачи всегда обладает некоторыми потерями. Поэтому входное сопротивление короткозамкнутого отрезка любой длины не будет бесконечно большим, как это имеет место

для идеальной линии, а будет иметь резко выраженные максимумы для длин /, удовлетворяющих условию (2.131).

Определим величину входного сопротивления реального ко-роткозамкнутого отрезка линии длиной в четверть волны. Входное сопротивление короткозамкнутой линии длиной / определяется по формуле Zo=ZBthY/=ZBth(a/+i р/). При l=klA и р/=л/2

Z„ = Z„th

= Z„cthaZ.

(2.133)

Если принять, что линия обладает небольшими потерями, то величина al мала и можно принять, что ctha« 1/а/. Тогда

макс«-г,/а/. (2.134)

Это выражение показывает, что входное сопротивление четвертьволнового короткозамкнутого отрезка реальной линии активно и величина его тем больше, чем меньше коэффициент затухания линии а. При длинах линии, равных ЗЯ/4, 5Я/4 и т. д., также будет справедлива ф-ла (2.134), а следовательно, входное сопротивление их будет большим. Однако наибольшим будет входное сопротивление отрезка длиной в четверть волны, так как его р.оэф-фициент затухания будет наименьшим.

/Линимальными значениями входного сопротивления будут обладать отрезки, длина которых удовлетворяет условию (2.132). Для «их al = kn, а входное сопротивление

Zo = ZJh{al + if2) = ZJhal. (2.135)

Принил!ая, что а мало, можно написать >

Z,,,,Z,al. (2.136)

Таким образом, входное сопротивление короткозамкнутой линии в зависимости от длины изменяется от Zomuh до ZoMaKc На рис. 2.23 показано изменение входного сопротивления коротко-замкнутой линии в зависимости от ее длины.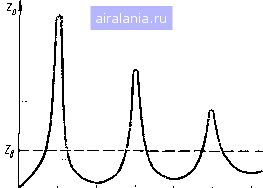

Рнс. 2.23. Изменение модуля в.чодного сопротивления реальной коротко-за.мкнутой линии от ее

ДЛ1!!Ы

Если короткозамкнутая линия имеет фиксированную длину 1 то она будет иметь бесчисленное множество резонансных частот (длин волн Ярй), определяемых из выражения (2.131):

Яр = 4г/(2.-1) (k=l, 2, 3...). (2.137>

Наиболее резко резонансные свойства короткозамкнутой реальной линии выражены на волне Xpt=4l, которая называется-основной резонансной волной. Входное сопротивление линии на этой волне в соответствии с ф-лой (2.134) равно

/?pi = 4Z3/aV. (2.138>

В отношении частотной зависимости сопротивления вблизи основной резонансной волны, как видно из рис. 2.23, короткозамкнутый отрезок реальной линии подобен параллельному колебательному контуру. На основе этого, используя зависимость сопротивления параллельного контура от расстройки, можно получить формулу для определения добротности короткозамкнутой реальной-линии.

Зависимость сопротивления параллельного контура от расстройки, как известно [4], определяется выражением

IZJ = •Р (2.139>

где Rkp - резонансное сопротивление параллельного контура;

Qk - добротность контура; = -----относительная расстрой-

ка контура.

Входное сопротивление короткозамкнутой реальной линии можно записать так:

Имея в виду, что а>1 мало, можно принять ihaloial, тогда

Z,n ~ i-n----

1-f iaHgPZ

a ; 1 + i a Hg P Z

Ввиду малости величины а/ ею можно пренебречь по сравнению с tgp/. Используя выражение (2.138) и равенство /=Xpi/4, получаем

= -]- •

Zo - pi

1 -f i а р /

i а/tgp/

Модуль этого выражения будет равен

ocMgp;