

|
|
Главная -> Радиочастотные линии 0 1 2 3 4 5 6 7 8 9 10 11 12 13 [14] 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 Вблизи основной резонансной частоты 2л,1 2 лЯ,р1/4 я/ Л " Я, " 2/р1 Поэтому Тогда \Zo\ = Л pi + А/ JL п 4- El 2 hi 2 (2.140) Сравнивая это выражение с выражением (2.139), можно видеть, что они будут тождественны, если добротность отрезка линии удет равна д„ = я/аЯр1. (2.141) Таким образом, входное сопротивление отрезка линии вблизи основной резонансной частоты выражается формулой Выражение (2.141) показывает, что добротность четвертьволнового короткозамкнутого отрезка линии будет тем больше, чем меньше его затухание. Если, например, затухание коаксиальной линии на основной резонансной волне lpi = 40 см равно 8,7-10-*1/м, то добротность четвертьволнового резонатора будет равна 9000. В диапазоне сверхвысоких частот невозможно получить резонансные системы с сосредоточенными параметрами, обладающие столь высокими значениями добротности. Полоса пропускания частот для четвертьволнового отрезка линии вблизи основной резонансной частоты определяется по формуле 2А/л = /р1/(Эл = а1;/л, (2.142) где у - скорость распространения электромагнитной волны в линии. 2.11. ЭКВИВАЛЕНТНЫЕ ПАРАМЕТРЫ КОРОТКОЗАМКНУТОЙ ЛИНИИ Определим параметры колебательного контура, эквивалентного резонансному отрезку короткозамкнутой линии (рис. 2.24). Для того чтобы два резонансных элемента были эквивалентными, необходимо равенство их резонансных частот, резонансных сопротивлений и полос пропускания частот. Обозначая эти величины для короткозамкнутого отрезка линии соответственно /р.л, Rp.n, Рис. 2.24. Контур, эквивалентный короткозамкнутому четвертьволновому отрезку линии (2.143> 2А/п.л, а для контура /р.к, /?р.к, 2А/п.к, можно написать: /р.л= /р.к = /р, .?р.л = ?р.к = .?р> 2А/„.л = 2А/„.к = 2А/„. Эти значения для короткозамкнутого отрезка линии могут быть выражены через основные параметры линии следующим образом: /р.л = 1Ар; /?р.л = 4Л,Мр; 2А/п.л = 1АрР = а1/я. (2.144) Аналогично для эквивалентного контура можно написать: /р.к= 1/2я] 7Сз; R,, = LJR,C,; 2 А/„.« = ?з/2 л 4. (2.145) Для определения эквивалентной емкости Сэ возьмем произведения 2А/п.к,?р.к= 1/2яСэ и 2Д/п.лр.л = 412в/я?1р. Так как левые части этих равенств равны в силу (2.143), то и правые части должны, быть равны. Отсюда находим С, = XlSv Z, = 1/8 ZJ. (2.146) Индуктивность эквивалентного контура из ф-л (2.145) будет равна --..-Л 4=1/4дСз = 22з/я7р. (2.147) Сопротивление потерь эквивалентного контура может быть определено из ф-лы (2.145): R, = L3/C3 i?3 = 41; а Zjn /р. (2.148) Полученные формулы показывают, что значения Сэ, La, Ra обратно пропорциональны резонансной частоте. Следовательно, для уменьшения параметров эквивалентного контура необходимо увеличивать резонансную частоту. Значительное уменьшение сосредоточенных емкости и индуктивности ограничивается наличием в схемах паразитных реактив-ностей. Кроме того, с увеличением частоты возрастает сопротивление потерь. Благодаря этому резонансные свойства систем с сосредоточенными и распределенными параметрами различны. В .диапазоне дециметровых и сантиметровых волн наиболее целесообразно использовать резонансные системы с распределенными лараметрами. 2.12. ТРАНСФОРМИРУЮЩИЕ СВОЙСТВА ЧЕТВЕРТЬВОЛНОВОГО ОТРЕЗКА ЛИНИИ Входное сопротивление линии без потерь длиной Я/4, нагруженной на активное сопротивление Ri, равно также активному сопротивлению R2. В соответствии с ф-лами (2.99) и (2.108) можно написать, что R2=ZJRi. Таким образом, четвертьволновый от-, резок может трансформировать активное сопротивление Ri в активное сопротивление Rz- Это важное свойство можно использовать, например, для согласования волновых сопротивлений. Допустим, надо согласовать две нагруженные линии с волновыми сопротивлениями Zbi и ZbZ. .Для этого оказывается достаточным включить между ними четвертьволновый отрезок линии (рис. 2.25) с волновым сопротивлением Zb3=ZbiZb2. в этом случае входное сопротивление со сто- 7ег- 1ная I вЗ 81 62 (82 Линия и Рис. 2.25. Согласование волновых сопротивлений с помощью четвертьволнового отрезка роны линии / будет равно ZBxi==Z\3lZbZ=ZbiZB2jZb2=ZBU а со стороны линии - Zb2 = Zbs/Zbi = ZbiZbs/Zbi = Zb2. Следовательно, две линии оказываются согласованными. Четвертьволновый отрезок можно использовать также для согласования нагрузки с линией. Для этого с помощью коротко-замкнутого отрезка соответствующей длины, подключаемого параллельно нагрузке, компенсируют ее реактивную составляющую. jHeждy скомпенсированной нагрузкой, представляющей уже чисто активное сопротивление, и линией включают четвертьволновый отрезок, обеспечивающий трансформацию скомпенсированной нагрузки в волновое сопротивление линии. Длина шлейфа /ш для компенсации реактивной составляющей нагрузки может быть определена следующим образом. Сопротив-.ление нагрузки необходимо пересчитать в проводимость. Допустим, что yi=Gi-iBi. Реактивная компонента проводимости нагрузки Bi должна быть скомпенсирована входным сопротивлением короткозамкнутого отрезка, т. е. необходимо, чтобы - iBi + Ч-1/i Хш = 0. Входное сопротивление короткозамкнутого отрезка определяется по ф-ле (2.67) и равно iXm=iZBtg р/щ. Используя, это равенство, получим В, = - -ctgpZ„j или ctgpZ„ = -B,Zb. (2.149> Из этих формул легко определяется длина короткозамкнутого шлейфа 1т- Входное сопротивление скомпенсированной нагрузки; будет Ri=\IGi. Рпс 2.26. Согласование нагрузки с волновым сопротивлением линии Полученное активное сопротивление Ri можно трансформировать в волновое сопротивление Zb. Это можно сделать путем включения четвертьволнового отрезка линии (рис. 2.26). Волновое сопротивление этого отрезка определяется по формуле Z; = K. (2.150) где Zb - волновое сопротивление линии. Рассмотренные способы обеспечивают точное согласование-только для одной частоты, соответствующей Я/4. В случае применения четвертьволнового трансформатора в широком диапазоне частот потребовалось бы изменять длину перехода. Это приведет к значительному усложнению при обслуживании такой линии. В настоящее время разработаны широкополосные трансформирующие переходы, которые сохраняют свои трансформирующие-свойства в широкой полосе частот, не требуя перестройки. Простейший широкополосный трансформирующий переход состоит из двух четвертьволновых отрезков, включенных последовательно. 2.13. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ЛИНИИ Коэффициент полезного действия (КПД) линии определяется: как отношение мощности на выходе линии (на приемном конце) к мощности на входе (на передающем конце). Если обозначить-Pi мощность, расходуемую в нагрузке, а Ял мощность потерь, рассеиваемую в линии, то КПД будет равен r\ = Pil{Pi + Pn). (2.151) Мощность, поглощаемая активной нагрузкой R, будет равна P, = U]/2R, (2.152> где Uim--максимальное значение напряжения на нагрузке. Используя ф-лу (2.48) и учитывая потери в линии, можно написать [/;,„ = £me-°V(l-НКБВ), где - амплитуда ЭДС питаю- едего источника. Подставив это значение в ф-лу (2.152), получим (2.153) 2i?(l--KBB)= Потери мощности в линии можно представить следующим выражением: Рл = (Рпзд - PbJ + (о.р - Рог,) (2.154) тде Рпад - мощность падающей волны в начале линии, равная /э„ад= {7223; Рпад - мощность падающей волны в конце ли- «ии, равная р;.д =-е-«; Ротр, Рохр- мощности отра- женной волны в начале и конце линии, соответственно равные: От g-2» f-oip "-P 22в Подставляя соответствующие значения в ф-лу (2.154), можно .написать p„ = i(l e-»)+-(l-e-"). 2Zb 2 Zb Амплитудные значения напряжения падающей и отраженной .волн, можно записать так: tnm- 2 • 0™ ™2(1+КБВ) Подставляя эти значения в формулу для Рл> получаем " 8Zb Ч (1 + КБВ) J Используя выражения (2.153), (2.155) и (2.151), получаем следующее выражение для КПД: R(l+KBB) 4 Zee ,-2 а г „-2 а/ (1-КБВ) 2„г (1 +КБВ)= Полагая, что R<Z, а iR/Zb = КБВ, получаем КБВ(1 +КБВ) „-2 а г (1-е-») (1-КБВ) 2а/ (1 + КВВ)2 (2.156) Максимальное значение КПД будет иметь линия при согласованной нагрузке, т. е. при КБВ = 1. Тогда -2а/ 1 Лмако = е „2 а / (2.157) При малых значениях затухания в линии формулы для КПД упрощаются и принимают вид 1 -I-(КБВ+ 1/КБВ) а/ l-l-(KCBH-M/KCBH)ai -. (2.158> W= 1/(1+2а0- (2.159> Коэффициент полезного действия можно выразить через модуль коэффициента отражения Г. Для этого используем выражения (2.45), (2.156) и (2.157). Произведя необходимые преобразо-вания, получим Лмакс- (2.160) 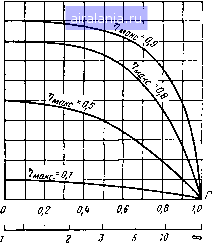 1,2 1,5 Рис. 2.27. Зависи.чость коэффициента полезного действия от коэффициента отражения На рис. 2.27 показана зависимость КПД от коэф-фициента отражения при различных значениях т]макс. Здесь же приведена шкала коэффициента стоячей волны. Из этого рисунка видно, что уменьшение КПД при наличии стоячей волны незначительно, если КСВН невелик. Так, например, если при отсутствии стоячей волны (КСВН = 1) КПД равен 80%, то он уменьшается лишь до 72% при КСВН = 3. При больших значениях КСВН величина КПД сильно падает. Таким образом, наличие стоячих волн в линии при КСВН, не превышающем 3, не оказывает существенного влияния на коэффициент полезного действия линии передачи. 2.14. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЛИНИИ ПО МЕТОДУ ХОЛОСТОГО ХОДА И КОРОТКОГО ЗАМЫКАНИЯ Вторичные и первичные параметры однородной линии можно определить по измеренным значениям сопротивлений холостого хода и короткого замыкания. Зная сопротивление холостого хода Zcx, и короткого замыкания Zo из ур-ний (2.52) и (2.53), можно определить волновое сопротивление Z3 = VZ, или IZ3I е = е . (2.1б1> 0 1 2 3 4 5 6 7 8 9 10 11 12 13 [14] 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 0.0114 |