Из этого выражения следует, что волновое сопротивление мож->яо определить как среднее геометрическое из сопротивлений холостого хода и короткого замыкания. Из ур-ний (2.52) и (2.53) следует также, что

thyl = VzJz: = th(al + ipi). (2.162)

Для определения коэффициентов затухания а и фазы р выполним некоторые преобразования. Введем обозначение th у / = Ге* и выразим гиперболический тангенс через показательные функции

<Ро-Ф»

thyl =

= /е*

где T = \YZo!Z„\; Ф< = (Фо - Ф«)/2.

Отсюда можно получить, что

2У1 1 +Те

е =

1 -Те

yl = al + \l = 4-In

1 +Те

1 Ф/

I-Ге

(2.163)

(2.164)

Подставляя в эту формулу значения Т и цц, которые выражены через Zo и Zoo, можно определить al и р/, а следовательно, аир при известной длине линии I.

В тех случаях, когда требуется определять только а или р, удобно пользоваться следующими формулами, получаемыми из (2.163):

Ш2аг = 2ГсозфД1 + Я), tg2pг = 2Tsiпф,/(l-n.

Отсюда

21 1

-Arth

2 Г cos ц>1

arctg

1 +Г 2Г5{пф( 1 -

-j- кя

(2.165) (2.166)

(2.167) (2.168)

Из этих формул видно, что при вычислении коэффициента фазы получается многозначное решение, обусловленное наличием слагаемого кя. Следовательно, необходимо выбирать соответствующее значение коэффициента k в ф-ле (2.168).

Для определения k нужно приблизительно З1нать теоретическое

значение р. Допустим, что р-р. Тогда 2р/« arctg /" +кя.

Отсюда * = (2p/-arctg{).

Полученное значение к необходимо округлить до ближайшего целого числа, так как оно равняется целому числу полуволн, укладывающихся в длине измеряемой линии. Для определения приближенного значения р можно одно из измерений произвести при такой длине линии, которой заведомо соответствует к=0.

При измерении параметров линии на высоких частотах для определения приближенного значения р можно пользоваться .формулой =ioVLC. При использовании формулы (2.164) для определения коэффициента фазы р к аргументу комплексного числа, выраженного правой частью ф-лы (2.163), необходимо добавлять слагаемое, равное 2кп.

Определив таким образом вторичные параметры линии Zb, у, чх й р, нетрудно рассчитать и ее первичные параметры iR, L, С я G. Используя выражения (2.19) и (2.20), можно написать ZbY= =i? + icoL, Y/ZB==G + icoC. Обозначив ZbY= IZbyIc и y/Zb= = Y/ZBe"» , получим:

/?-lvZJcostJ,i, (2.169)

(2.170)

= - IVBlsinaJji,

cos г1?2,

sin \pg.

(2.171) (2.172)

Необходимо отметить, что при значительном коэффициенте затухания измеряемой линии ее входные сопротивления при холо-•стом ходе и коротком замыкании мало отличаются друг от друга. Это ведет к уменьшению точности, с которой могут быть определены вторичные и первичные параметры линии. Практически метод холостого хода и короткого замыкания рекомендуется применять для определения параметров линий, затухание которых не превышает 8-10 дБ.

2.15. ПЕРВИЧНЫЕ ПАРАМЕТРЫ ДВУХПРОВОДНОЙ ЛИНИИ

Под двухпроводной линией будем понимать линию передачи электрической энергии, выполненную из двух параллельных проводников. Такие линии очень широко применяются для передачи электрических сигналов связи низкой частоты на большие расстояния. Основным преимуществом этих линий является простота конструкции.и удобство соединения с симметричными нагрузками.

Для радиочастотных линий передачи двухпроводная линия применяется сравнительно редко. Это объясняется тем, что электромагнитное поле двухпроводной линии (рис. 2.28) не экранировано и при длинах волн, соизмеримых с расстоянием между проводни-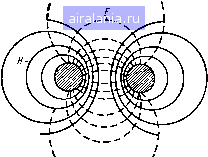

Рис. 2.28. Структура электромагнитного поля (двухероводной линии в по-переч"ном сечении

ками, резко возрастают потери при излучении. Кроме того, с повышением частоты сильно увеличиваются потери в проводниках и изоляторах, служащих для- подвески проводников. Однако в ряде

случаев применение двухпроводных линий на длинных, коротких,, а иногда и метровых волнах является выгодным.

В общем случае электромагнитное поле двухпроводной линии будет многоволновым. В линии могут распространяться как поперечно-электромагнитные волны типа ТЕМ, так и при определенных условиях волны высших типов. Поскольку неоднородности и изгибы двухпроводных линий сильно влияют на распространение волн высших типов, то их изучение не представляет пока практического (интереса. Поэтому, если специально не оговаривается, здесь рассматривается лишь распространение волн типа ТЕМ, являющихся основным типом для двухпроводной линии.

Двухпроводная линия передачи не обладает цилиндрической симметрией, и при строгом решении задачи нельзя использовать цилиндрическую систему координат. Попытки применить биполярную систему координат [1, 2], как показывает анализ [3], также не дают практически приемлемых результатов для точного описания электромагнитного процесса в двухпроводной линии.

Для решения инженерных задач при рассмотрении полей двухпроводной линии можно использовать и цилиндрическую систему координат. Однако при этом приходится прибегать к некоторым допущениям и решать задачи в известной степени приближенно [4, 5, б, 7]. Однако эти приближения вполне допустимы, так как получаемые результаты расчетов хорошо совпадают с экспериментальными данными.

При передаче по двухпроводной линии токов высоких частот внутри и снаружи проводников возникает переменное магнитное поле. Это поле наводит разные электродвижущие силы в отдельных точках сечения собственного я соседнего проводников. Под действием электродвижущих сил в проводниках возникают вихревые токи, которые вытесняют рабочий ток на поверхность проводника. Это явление называется поверхностным эффектом и рассмотрено в разд. 1.7. Вихревые токи в соседнем проводнике смещают текущий в нем обратный ток по направлению к прямому току (рис. 2.29). Это явление называется эффектом близости, или эффектом сближения. Эффект близости приводит к увеличению сопротивления и уменьшению индуктивности двухпроводной линии. 94

Влияние эффекта близости можно не учитывать при низких частотах и сравнительно большом удалении проводников линии друг от друга. В этом случае для расчета сопротивления и внутренней индуктивности проводников линии можно использовать формулы разд. 1.7.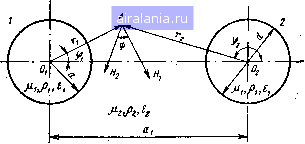

Рис. 2.29. Эффект близости в двухпроводной линии

Расчет сопротивления и внутренней индуктивности двухпроводной цепи с учетом эффекта близости представляет известные трудности. Как отмечалось выше, эта задача может быть решена в известной степени приближенно. При решении ее примем, что токи смещения в проводниках отсутствуют, а токи проводимости в диэлектрической среде, окружающей проводники, равны нулю. Будем рассматривать только поперечные электромагнитные волны, так как они внутри проводников текут только в направлении оси проводника, принимаемой за ось z. В этом случае из шести составляющих электрического и магнитного полей останутся только три: Ег, Иг и Яф. Эти составляющие определяются ур-ниями (1.159) - (1.161). Дифференцирование этих уравнений дает ур-ние (1.161), решением которого является следующее выражение:

cos П ф.

(2.173)

Для составляющей И - напряженности магнитного поля в проводнике- можно написать

5] [An In iVikr) + Б„ Кп iVikr)] cos n ф,

(2.174)

где /„, Кп - функции Бесселя соответственно первого и второго рода п-го порядка; An, В,, - постоянные интегрирования.

С физической точки зрения ур-ния (2.173) и (2.174) описывают основное поле, созданное током в одиночном проводнике («=0), на которое наложены поля, зависящие от угла ф и совданные вихревыми токами как в рассматриваемом, так и соседнем проводниках. Сюда же входит и основное поле соседнего проводника, рассматриваемого как одиночный. Наличие множителя cos п ф при-

водит все составляющие к основной составляющей поля рассматриваемого проводника. В результате сложения полей суммарное поле в проводнике будет искаженным и центры электрического и магнитного полей сместятся относительно геометрической оси проводника. Отсюда следует, что выражения (2.173) и (2.174) дают возможность учесть действие эффекта близости.

Для диэлектрической среды, в которой отсутствуют объемные электрические заряды (div£=0), правая часть ур-ния (1.162) будет равна нулю. Поэтому ур-ние (l.il62) можно переписать так:

Г дг /-2

(2.175)

дг» г дг

Это дифференциальное уравнение, называемое уравнением Лапласа, может быть решено методом разделения переменных. В результате решения получается

£,д = С, 1п г 4- Do -f (С„ г" + D„ Г") cos п ф.

(2.176а)

Имея в виду, что

дЕг дг

= i (1) fia Яф , получим

Яф д -

id) Но

+ У] - (С„ г"- - D„ г-"-) cos п ф. (2.1766)

Это выражение показывает, что напряженность магнитного поля с увеличение.м координаты г может не только уменьшаться,

7 но и возрастать. Однако напряженность магнитного поля за пределами рассматриваемой системы проводников с увеличением расстояния должна уменьшаться. Поэтому решение ур-ний (2.176) может быть справедливо лишь для ограниченной области. Определим эту область, полагая, что Яфд создано токами проводников 1 и 2 (рис. 2.30), составляющими электрическую цепь. В этом случае напряженность магнитного поля Н фд можно рассматривать как сумму напряжен-токами в обоих проводниках (см. рис. 2.30) можно напи-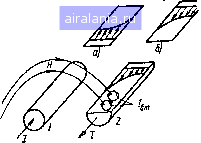

Рис. 2.30. К расчету электро.маг-нитиого поля двухпроводной линии

ностей Hi и Нп, созданных цепи. Поэтому для точки А

сать фА = Я1-ьЯ2С05ф. Если 15<.п/2, toHa>Hi иг,<1>со5ф; если \;>я/2, то Н a<Hi и Г1>Дсо8ф; если i3=ji/2, то ЯфД = =Hi и Л) =Z) cos ф.

Следовательно, границей области будет Го=0 cos <р. Для области г>Го необ.чодимо принять Сп=0. Тогда, как видно из ур-ния С6

(2.176), уравнение для Яфд будет содержать лишь члены, убывающие с возрастанием г. Но тогда оно не будет пригодно для области г<СГо. Следовательно, оба решения могут дать практически точные результаты лишь в том случае, если рассматривать точки, достаточно удаленные от области Го=В cos ф. Эти ограничения и неточности связаны с использованием цилиндрической системы координат.

Постоянные интегрирования Л„, Вп, Сп н Dn могут быть определены из граничных условий, согласно которым напряженности магнитных и электрических полей на поверхности проводника будут равны друг другу. Кроме того, необходимо использовать условие, согласно которому напряженности магнитного поля проводников / и 2 (см. рис. 2.30) в точках, отстоящих на одинаковых расстояниях от проводников, должны быть равны друг другу.

Определив постоянные интеприрования, можно рассчитать сопротивление и внутреннюю индуктивность двухпроводной цепи, исходя из напряженности электрического и магнитного полей на поверхности .проводника:

R = f [Е, (а) я; (а) + El (а) Я (а)] ad ф, (2.177)

- j [EAa)H;{a) + El(a)H(a)]ad<f. (2.178)

Производя соответствующую подстановку и необходимые преобразования, получим следующую формулу для расчета сопротивления двухпроводной цепи R, Ом/м, с учетом эффекта близости:

G(ka)(d/ai)

1 +F(ka) +

l - Н (ka) (d/aj) J

(2.179)

где Ro - сопротивление одного провода цепи постоянному току, Ом/м; F(ka) - коэффициент, учитывающий сопротивление, эквивалентное потерям на вихревые токи, возбуждаемые внутренним магнитным полем; G(а) - коэффициент, учитывающий сопротивление, эквивалентное потерям на вихревые токи, возбуждаемые внешним магнитным полем в обратном проводе; Я(/а)-коэффициент, учитывающий сопротивление, эквивалентное потерям на вихревые токи, возбуждаемые вторичным магнитным полем в обратном проводе.

Значения коэффициентов F(ka), G(ka) и H(ka) в зависимости от величины ka приведены в табл. 2.1.

Величина ka для медных проводников может быть вычислена по формуле

ka = O,0l0bdVT, (2.180)

где d - диаметр проводника, мм; / - частота тока, Гц. 4-320 97