

|
|
Главная -> Радиочастотные линии 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [16] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 Таблица 2.1 Значения коэффициентов F(ka), G(ka), H(ka) и Q(ka)
Для частот свыше 1 МГц для инженерных расчетов ф-ла (2.179) может быть значительно упрощена и приведена к виду 4-10 У 10 1 / d (2.181) где /? -активное сопротивление, Ом/м; d -диаметр проводников, мм; \i. - относительная магнитная проницаемость материала проводников; р -удельное сопротивление проводников, Ом-мм/м; Ох - расстояние между проводниками, мм. Для медных проводников активное сопротивление R, Ом/м, определяется по формуле R = 0,167. lo- 1 + (2.182) Внутренняя индуктивность проводника Li, Г/м, с учетом влияния эффекта близости может быть определена по формуле Lt=-Qika)-lO-,. . (2.183) где Q(ka) - коэффициент, учитывающий влияние эффекта близости, определяемый по табл. 2.1. Общая индуктивность цепи будет складываться из внутренней индуктивности двух проводников 21, и внешней индуктивности Lc, т. е. индуктивности между проводниками: L==2Li-\-L,. (2.184) Внешняя индуктивность двухпроводной цепи может быть определена по формуле (2.185) Подставляя в эту формулу соответствующее значение Яфд, после интегрирования получим jr = 4lnii-10- = 9,21gi (2.186) {Le измеряется в генри на метр). Для определения емкости двухпроводной цепи необходимо определить разность потенциалов между проводниками 1 и 2. Разность потенциалов между указанными проводниками, создаваемая зарядом q в проводнике 1, будет равна а,-а в,-а " l dr = -Ini, (2.187) 2л 8а 2 Я Ео е а где а, - расстояние между проводниками цепи, мм; а - радиус проводника, мм; 8 - относительная диэлектрическая проницаемость среды между проводниками. Полагая, что разность потенциалов, создаваемая зарядом q в проводнике 2, будет иметь такую же величину, получим U=2Ui. Тогда емкость между двумя проводниками будет равна а,-а в,-I С- - - 2л8„е а, - а 36 In а, ~а или С, нФ/м, равна С = ЯЕЕп (2.188) Проводимость изоляции двухпроводной линии зависит от сопротивления изоляции и диэлектрических потерь и определяется по формуле G = Go + o)Ctg6= l ?„3 + «Ctg6, (2.189) где /?из - сопротивление изоляции при постоянном токе между проводниками / и 2; tg б - тангенс угла диэлектрических потерь. Учитывая высокое значение сопротивления изоляции R, первым членом в ф-ле (2.189) обычно пренебрегают. В случае воздушной линии tg б зависит от изоляторов и воздуха, окружающего проводники, а следовательно, и от метеорологических условий. В этом случае рекомендуется пользоваться при расчетах следующей эмпирической формулой: G=--G, + nf, (2.190) где п-коэффициент, учитывающий потери в диэлектрике и равный 0,05-10-3 для сухой погоды и 0,25-10- для сырой погоды; / - частота тока, Гц. Значение проводимости изоляции Go при постоянном токе рекомендуется брать равным 0,l•10- См/м для сухой погоды и 0,05-10- См/м для сырой погоды. 2.16. ВТОРИЧНЫЕ ПАРАМЕТРЫ ДВУХПРОВОДНОЙ ЛИНИИ Вторичными параметрами двухпроводной линии являются волновое сопротивление 2в, коэффициент распространения у, коэффициент затухания а и коэффициент сдвига фаз р. Если известны первичные параметры линии, то вторичные параметры могут быть определены по ф-лам (2.19) и (2.20). При высоких частотах можно использовать ф-лы (2.23), (2.24) и (2.33). Подставив в ф-ле (2.33) значения L а С из формул (2.186) и (2.188), получим следующую формулу волнового сопротивления в зависимости от конструктивных параметров двухпроводной линии: у г d Уг d Уг d (2.191) В случае если проводники цепи имеют различные диаметры d, и 2 (несимметричная линия), то волновое сопротивление подсчи-тывается по формуле 2ai 276 , 2oi 7 20 Z„ = -- In У г °yd,d- (2.192) На рис. 2.31 показана зависимость [25] волнового сопротивления двухпроводной линии от отношения ajd. Коэффициент затухания двухпроводной линии при высоких частотах можно определить по формуле a=R/2ZB + GZs/2. Подставляя в эту формулу значения R из ф-лы (2.181), Zb нз ф-лы (2.191) и имея в виду, что G = coCtg б, получаем, дБ/м 45,5-10~ \lipf I 1 2ai-d d \ + 10-8/K6tg6. (2.193) В случае медных проводников и воздушного диэлектрика коэффициент затухания а, дБ/м, может быть определен по формуле 2,6-lO-Q +9,08/tg б. (2.194) При высоких частотах двухпроводная линия будет излучать некоторое количество энергии. Дополнительное значение коэффициента затухания в децибелах вследствие излучения для длинных 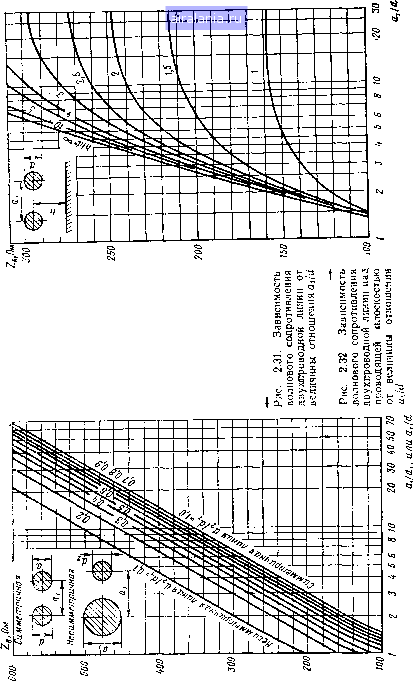 прямых линий может -быть определено по следующей [26] приближенной формуле: al = 6900 где Я - длина волны. На рис. 2.32 показана зависимость волнового сопротивления двухпроводной линии над проводящей плоскостью от величины отнощения ajd. Представляет интерес определение волнового сопротивления многопроволочных линий передачи. На сверхвысоких частотах эти линии обладают нестабильностью свойств распространяющихся волн вследствие многочисленности комбинаций проводников, соответствующих различным волнам. Однако на более длинных волнах эти линии находят практическое применение. В случае симметричной четырехпроводной линии возможно несколько вариантов возбуждения. На рис. 2.33 приведена зависи- 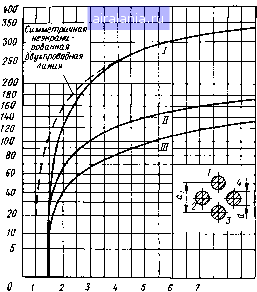 Рис. 2.33. Зависимость волнового сопротивления четырехпроводной линии от величины отношения S 9 add a,ld мость волнового сопротивление четырехпроводной линии от отношения Qi/rf для наиболее важных вариантов возбуждения [25]. Кривая / соответствует случаю, когда проводники 7 и <? образуют двухпроводную линию, а проводники 2 W 4 - нейтральное окружение; кривая - двухпроводную линию, образованную соединенными проводниками 1 ш 2 в качестве одного, 3 я 4 в качестве другого проводника; кривая / - двухпроводную линию, образованную соединенными проводниками / и <? в качестве одного w 2,4 в качестве другого проводника. Следует отметить, что третья комби- нация имеет сравнительно низкое волновое сопротивление, близкое к волновому сопротивлению коаксиального кабеля. Поэтому данная комбинация находит наибольшее практическое применение. Волновое сопротивление Zb, Ом, для случая кривой / может быть определено по следующей приближенной формуле [25]: z. = -ia (2.195) Эта формула справедлива при djai<0,5. Двухпроводная линия может быть образована из комбинации шести (рис. 2.34а) и восьми (рис. 2.346) проводников. Волновое Рис. 2.34. Линии передачи 113 шести (а) и восьми (б) проводннкав 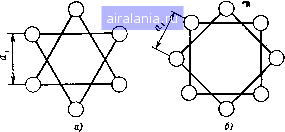 сопротивление для проводников на рис. 2.34а приближенно под-считывается по формуле (2.196) (2.197) Z„ = 40 In а для проводников на рис. 2.346 -по формуле Z„ = 30 in l,3ai где d -диаметр проводника. 2.17. ДВУХПРОВОДНАЯ ЛИНИЯ ИЗ БИМЕТАЛЛИЧЕСКИХ ПРОЮДНИКОВ Параметры цепи из биметаллических проводников могут быть рассчитаны по тем же формулам, что и параметры цепи из монометаллических проводников, за исключением сопротивления и внутренней индуктивности. Определим сопротивление и внутреннюю индуктивность цепи из биметаллических проводников, показанной на рис. 2.35. При решении этой задачи целесообразно рассматривать два случая расчета: с учетом эффекта сближения и без учета его. Сопротивление п внутренняя индуктивность биметаллического проводника без учета эффекта сближения могут быть определены по ф-ле (1.218). 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [16] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 0.0125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||