Однако эта формула сложна для практических расчетов. Для ее упрощения введем обозначения:

1 <Pi «1

«8

азе* = -.

(2.198) (2.199)

Тогда ф-лу (1.218) нетрудно преобразовать и выделить из нее действительную часть, характеризующую сопротивление биметал-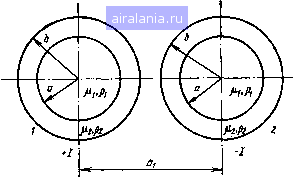

Рис. 2.35. Двухпроводная линия из биметаллических проводов

лического проводника R, и мнимую часть, характеризующую внутреннюю индуктивность Li. Производя соответствующую подстановку, получаем:

R = R„q4, (2.200)

(2.201)

В этих формулах Ro = p2/nb-сопротивление постоянному току проводника радиуса b с удельным сопротивлением рг; q=bfa;

«2 cos (qpi-fср2)+"Дг (cos (fi-f(p)-f«г «з cos ti]+"«ga cos (Ф1-fg)

I + 2rt аз a cos (фз-f Ф)-f «2 «2

(2.202)

k" = «2 sin (ф1-4-Ф2)+Д«2 [si" (ф1+ф)+«2аз sin t)),]-j-najgsin (ф - фз)

I -[-2я(Хзасо5(Фз -f-ф)-f naja

(2.203)

Выражения (2.202) и (2.203) показывакуг, что величины k и " - это функции двух переменных: yka и q. Величина q, характеризующая отношение радиуса биметаллического проводника к радиусу его внутренней части, является постоянной для данной конструкции. Величина у зависит от частоты тока. Таким образом, частотная зависимость коэффициентов ¥ и k", а следовательно, R и Li определяется изменением величины у.

Если биметаллический проводник выполнен из стальной проволоки, покрытой слоем меди с удельным сопротивлением 0,0175 Ом-ммм, то величина у может быть рассчитана по формуле i/= 2,124-10-2аК/, где а -радиус стального сердечника биметаллического проводника, мм; / - частота тока, Гц.

Задаваясь различными значениями у н q, можно рассчитать величины коэффициентов и при расчетах пользоваться ими. Значения величин «1, 02, аз и <pi, ф2, Фз табулированы [24].

Для определения влияния эффекта сближения необходимо учитывать составляющие напряженности электрического и магнитного полей от л=1 до п=оо ур-ний (2.173) и (2.174). Эти уравнения для случая биметаллического проводника можно записать так [23]:

для внутренней части биметаллического проводника (при 0<г<а)

Ег, = J] [An, In (Ki *1 г) + Вп, Кп (VTl г)] COS П ф,

/1=1

/; (VTi г) + Вп, Кп (УТк г)] COS п ф;

(2.204)

для наружной части биметаллического проводника (при а<г<Ь)

00 А

е.. - [An, L (Ki К г) + Вп, Кп iVTk, г)] cos п ф.

i *2Р2

An, In (yT2 ) + Вп, Кп (V2 )] COS П ф.

(2.205)

Для определения постоянных интегрирования необходимо по ф-лам (2.176а) и (2.1766) найти напряженность электрического и магнитного полей вокруг проводников цепи, т. е. в диэлектрике. При учете только эффекта сближения эти выражения будут иметь вид

(2.206)

Уравнения (2.204) - (2.206) содержат шесть постоянных интегрирования. Постоянная интегрирования Вп, = 0 из физических соображений [при г = 0 напряженность поля Яф, будет конечной ве-

личиной, а это может быть, как следует из ур-ния (2.204), при Bn ==0]. Для определения других постоянных интегрирования необходимо иметь пять уравнений. Четыре уравнения могут быть получены из условия равенства напряженностей электрического и магнитного полей на границах раздела, т. е. при г=а и г=6:

1) (а) = £,.(«). 2) Н{а) = НМ 3) Ег,{Ь)Е(Ь). 4) ЯфЛ6) = Яфд(6).

Эти уравнения дают возможность выразить четыре постоянных интегрирования через одну постоянную, например С„. Для определения постоянной интегрирования Сп можно воспользоваться условием, согласно которому напряженности магнитного поля в точках, отстоящих на одинаковых расстояниях от проводников 1 ш 2 (см. рис. 2.35), составляющих электрическую цепь, равны друг другу.

Таким образом, все постоянные интегрирования будут определены. Подставляя значения этих постоянных в ур-ния (2.205) и полагая г = 6, найдем напряженности электрического и магнитного полей на поверхности проводника:

COS П ф,

созггф.

В этих выражениях приняты следующие обозначения:

/1 kb

N„= I-

Ha2 Ho

1 ka J

?nPn,-[l +

gnPn,

Ha.

p„. = /„ {Y\n,a) Kn iVThb) - /„ Kn [VVk,al

Pn, == 4 Kn-i [УТкф) + In-x (Ki Kb) Kn (Ki -V),

Pn. = „ (VT*2*) 4-1 [VTha) + /„ (vT/,6) {уТка\ Pn. = /«-1 (КГ2) Kn-x iVka) - In-, {yVka) Kn-i (УГкф).

(2.207)

(2.208)

(2.209)

(2.210)

(2.211)

Используя выражения (2.177) и (2.178), можно определить сопротивление и индуктивность биметаллического проводника, обусловленное эффектом сближения:

Xi+Xi

т Но

Lib - -

где q =

1-IXi

ll-iXiSV 1-SV2 ai Ml

(2.212)

(2.213)

Значения JVi и Mj определяются no ф-лам (2.208) и (2.209), если в них положить п=1.

Таким образом, общее сопротивление R, Ом/км, и индуктивность L, Г/км, двухпроводной цепи из биметаллических проводников в соответствии с ф-лами (2.200), (2.212), (2.201), (2.213) и (2.186) могут быть определены так:

R = 2R„qk + F,),

9,2\g- + h{k"+F,)

(2.214) (2.215)

1 - t,V2

(2.216) (2.217)

Для конкретных сочетаний различных металлов биметаллического проводника могут быть составлены таблицы коэффициентов f 1 и р2, учитывающих эффект сближения.

ГЛАВА 3

РАСЧЕТ ПАРАМЕТРОВ КОАКСИАЛЬНЫХ РАДИОЧАСТОТНЫХ КАБЕЛЕЙ

3.1. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В КОАКСИАЛЬНОМ КАБЕЛЕ

Коаксиальный кабель (рис. 3.1) представляет собой совокупность двух изолированных друг от друга, соосно расположенных проводников (один в другом). Основными элементами коаксиального кабеля являются внутренний проводник, внещний проводник и диэлектрик между внутренним и внещним проводниками. Конструкция и материал каждого из этих элементов зависят от назначения и области применения кабеля.

в коаксиальном кабеле, используемом в качестве линий передачи электромагнитной энергии, возможно существование поперечно-электромагнитных волн типа ТЕМ, электрических волн типа Е и магнитных волн типа Н. Как отмечалось в первой главе, волны типа ТЕМ не имеют критических частот (/кр=0), поэтому по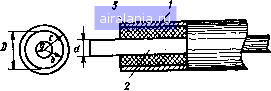

Рис. 3.1. Общий вид конструкции коаксиального кабеля:

/ - внешний проводник;

2 - внутренний проводинк;

3 - диэлектрик

коаксиальному кабелю могут распространяться колебания волн типа ТЕМ любых частот. Критические волны типов Е и Н соизмеримы с размерами кабеля и по коаксиальному кабелю могут распространяться только на очень высоких частотах.

Волна типа ТЕМ в коаксиальном кабеле называется волной основного типа, а все волны типов Е и Н -волнами высщих типов. В настоящей главе рассматривается распространение волн основного типа (если специально не оговаривается).

При анализе электромагнитных волн в коаксиальном кабеле наиболее целесообразно пользоваться цилиндрической системой координат с осями г, if и Z. Рассмотрим вначале идеализированную конструкцию кабеля, т. е. такой кабель, оба проводника которого по всей длине расположены точно коаксиально, контуры обоих проводников в любом поперечном сечении представляют собой окружности с постоянными диаметрами, а удельные сопротивления, магнитные и диэлектрические проницаемости обоих проводников и диэлектрика постоянны по длине кабеля.

При прохождении тока по проводникам коаксиального кабеля в нем возникает электромагнитное поле, которое описывается уравнениями Максвелла. Эти уравнения в цилиндрической системе координат при гармонических колебаниях определяются выражениями (1.20) и (1.21).

Предположим, что ось кабеля совпадает с z. Тогда вследствие цилиндрической симметрии электромагнитное поле не будет зависеть от координаты <р и все производные по <р будут равны нулю. Кроме того, по физическим соображениям будут отсутствовать составляющая Hz напряженности магнитного поля по оси z, тангенциальная составляющая напряженности электрического поля £ ф и радиальная составляющая напряженности магнитного поля Нг-Следовательно, для коаксиального кабеля останутся лишь составляющие электромагнитного поля Ez, Ег а Нц,.

На основе ур-ний (1.20) и (1.21) с учетом выражения (1.16) для электромагнитного поля коаксиального кабеля получаются следующие уравнения: 10S

-iEAo + шг),

дг дЕг дг

"л

+ lll = i?,(f + i«e), = -1а)раЯф.

(3.1) (3.2) (3.3)

Эти уравнения полностью характеризуют электромагнитное поле коаксиального кабеля идеальной конструкции как в проводниках, так и в диэлектрике.

Напряженность магнитного поля коаксиального кабеля содержит лишь одну составляющую Яф . Это означает, что линии магнитной индукции располагаются концентрически вокруг оси z. Электрическое поле характеризуется радиальной составляющей Ет, обусловливающей наличие тока смещения в диэлектрике, и продольной составляющей Ez, вызывающей ток проводимости в проводниках кабеля. Структура электромагнитного поля в коаксиальном кабеле показана на рис. 3.2. Вокруг кабеля идеальной конструкции электрическое и магнитное поля отсутствуют. Физически это следует из того, что внешнее поле создается токами противоположных направлений внутреннего и внешнего проводников.

Найдем выражения для составляющих поля в отдельных элементах коаксиа-тьного кабеля. В проводниках кабеля радиальная составляющая напряженности электрического поля Ег равна нулю. Кроме того, or>i(oeo. При этих условиях ур-ния (3.1) - (3.3) можно записать так: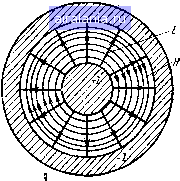

Рнс. 3.2. Распределение магнитного Н н электрического Е полей в коаксиальном кабеле

дг дг

Ф -

= 1(ор,оЯф,

(3.4) (3.5)

где ,р - удельное сопротивление проводника.

Производя дифференцирование ур-иия (3.5) и подставляя в

ур-ние (3.4) значения и Яф , получаем

дг» г дг

где k=V ЫЦа/р.

(3.6)