Согласно закону Джоуля - Ленца в дифференциальной форме величина аЕ выражает объемную плотность мощности. Поэтому второй член правой части равенства (1.38) выражает энергию,

преобразовываемую в тепло за единицу времени.

Таким образом, согласно теореме Умова-Пойнтинга изменение запаса электромагнитной энергии, находящейся в некотором объеме V, происходит за счет расхода энергии внутри объема и распространения энергии за пределы этого объема.

Направление .движения электромагнитной энергии в пространстве показывает направление вектора Умова-Пойнтинга 5. Направление вектора S определяется поступательным Рис. 1.2. Определение направ- движением буравчика, рукоятка кото-лвния вектора У.мова-Пойн- £ого ращается в плоскости векторов

Е и Н по направлению от вектора Е

к вектору Н (рис. 1.2).

Выражение [£Я]„ в ур-нии (1.38) представляет собой составляющую вектора Умова - Пойнтинга, нормальную к поверхности S.

В рассмотренном объеме V может иметь место приток энергии от CTopoHHHxjicT04HHKOB. Эта энергия может быть оценена выражением -j Ej-dV, где /ст - объемная плотность сторонних

токов. Сторонние токи - это такие токи, которые возбуждают поля, но сами не порождаются рассматриваемыми электромагнитными полями. В этом смысле они являются «сторонними» по отно-щению к полю.

С учетом энергии сторонних токов теорему Умова - Пойнтинга можно записать так:

Г EUdV = + aBdV+[EH]n ds. (1.40)

V V s

Данное выражение показывает, что мощность сторонних источников расходуется на изменение запаса энергии в объеме V, на джоулево тепло и на излучение энергии во внещнее пространство.

Уравнения (1.38) и (1.39) характеризуют мгновенные значения мощности. При гармонических колебаниях обычно оперируют со средними за период значениями мощностей. В этом случае среднее значение энергии за один период при установивщемся режиме равно нулю, т. е. dWcp/dt=0. Тогда ур-ние (1.40) применительно к средним значениям мощности можно записать так: 14

Ёи = -~ Re f £Я*аЛ +-Re[EH*Lds,

где звездочкой отмечено комплексно-сопряженное значение соответствующих величин; Re показывает, что необходимо брать вещественную составляющую соответствующих подынтегральных выражений.

1.3. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ДИЭЛЕКТРИКЕ

При рассмотрении электромагнитного поля в диэлектрике можно положить, что удельная проводимость о = 0. В этом случае ур-ния (1.9) и (1.10) можно записать так:

rot Я = e„

rot£ = - fi,

дН dt

(1.41) (1.42)

Используя эти равенства, можно получить следующие волновые уравнения:

V* Я = гЦа ,

(1.43) (1.44)

Рассмотрим наиболее простой случай распространения плоской электромагнитной волны в однородном и изотропном диэлектриках. Электромагнитная волна называется плоской, когда все величины, характеризующие интенсивность электромагнитного процесса, зависят только от одной декартовой координаты. Предположим, что в прямоугольной системе координат вектор Е направлен по оси у {Ех=Е, = 0) и что величина Еу изменяется толь-

/дЕи dE

ко вдоль направления х

У. = ЧВМ- = о

В ЭТОМ случае ур-ние (1.44) запищется так:

(1.45)

Решением этого дифференциального уравнения в общем случае является выражение, состоящее из двух функций:

Ey = F,(t-V7x) + F,{t+Vx), (1.46)

В частном случае функции Fi и Fz могут быть синусоидальными или косинусоидальными. Функция Fi выражает волнообразное изменение напряженности электрического поля, распространяющееся в сторону положительных значений х (падающая волна),

а функция Fz - B сторону отрицательных х (отраженная волна).

Скорость распространения волн зависит только от магнитных и электрических свойств среды и определяется выражением

f=l/Kiw (1.47)

пространстве скорость

При распространении волн в свободном

распространения v = !- З-Ю». м/с, т. е. равна

4Я-10

Збп-109

скорости света.

Используя второе уравнение Максвелла при тех же допущениях, можно получить

(1.48)

Рассматривая совместно ур-ния (1.46) и (1.48), можно заключить, что при распространении плоской электромагнитной волны в однородном и изотропном диэлектриках векторы Е и Н взаимно перпендикулярны. Из этих же уравнений следует, что отношение между величинами векторов Е и Н для падающих волн равно V[ia/га , а для отраженных волн равно - У nJ&a- Величина У]Ха1га имеет размерность электрического сопротивления, и ее называют волновым сопротивлением среды Zb. При распространении волн в свободном пространстве (и с достаточным приближением в воздухе) волновое сопротивление Zo, Ом, будет равно

4Я-10

1/36Я-10»

120лл; 377.

Величину энергии, переносимой электромагнитной волной, можно оценить с помощью вектора Умова - Пойнтинга. Допустим, что существует падающая электромагнитная волна, определяемая функцией Fu входящей в ур-ния (1.46) и (1.48). Полагая, что происходит гармоническое изменение величин, можно написать:

Е = EJ = £т sin со t--j

H = HJi = sin со

Вектор Умова - Пойнтинга будет равен S = {EH]=s\xi(Si{t--Y-

(1.49) (1.50)

(1.51)

Этот вектор направлен по оси х и совпадает с направлением движения электромагнитной волны (рис. 1.3). На рис. 1.3а показан один из способов изображения плоской электромагнитной волны для случая гармонического изменения величин Е я Н путем из-16

менения длин векторов поля. Применяются и другие способы изображения плоской электромагнитной волны. На рис. 1.4а показано изменение величин векторов поля путем изменения уровней густоты линий поля. Если необходимо изобразить конфигура-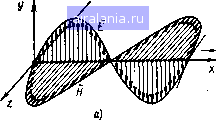

Рис. 1.3. Падающая плоская электромагнитная волна (а) и направление вектора Умова-Пойнтинга (б)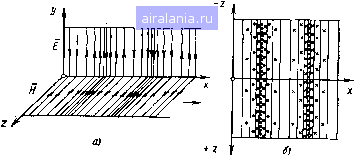

Рис. 1.4. Способы изображения плоской элекгромагнитной волны

цию волны в нормальной проекции, а не в виде перспективного рисунка, то удобно использовать точки и крестики для изображения векторов, нормальных к плоскости рисунка. На рис. 1.46 точками изображены векторы, направленные к наблюдателю; крестиками - от наблюдателя. Густота точек и крестиков пропорциональна напряженности поля.

При рассмотрении электромагнитного поля в диэлектрике иногда пользуются понятиями электрического и магнитного векторов Герца. Вектор Герца дает возможность выразить два вектора- Е и Я - через один вектор, являющийся функцией координат и времени. Используя уравнения Максвелла, можно показать, что электрический вектор Герца, равный при гармонических колебаниях

Z,= n,e", (1.52)

связан с векторами Н и Е следующими выражениями: T/rotWiwrotne

(1.53)

£ = - (grad div + аЧц Щ е

(1.54)

Магнитный вектор Герца, равный при гармонических колебаниях

связан с векторами Н и Е следующими выражениями: Я---- (grad div П„ -f (оЧаЦа ПJ е" ,

£ = rot = ia)rotn„e" dt

(1.55)

(1.56) (1.57)

Используя векторы Герца, можно получить следующие волновые уравнения:

VZ,-f a)4[.. = 0, (1.58)

V»Z„-f a)4fi,Z„ = 0. (1.59)

Векторы Герца и связанные с ними уравнения применимы к любой системе координат и, следовательно, являются универсальными.

1.4. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ПРОВОДЯЩЕЙ СРЕДЕ

В проводящей среде практически всегда можно пренебречь токами смещения по сравнению с токами проводимости. Тогда уравнения Максвелла (1.9) и (1.10) примут вид

го1Я = а£.

t.-B дН

(1.60) (1.61)

£а,Ма. 6¥0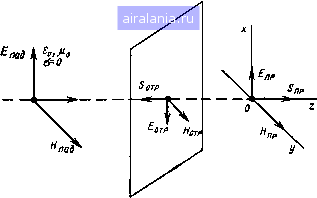

Рис. 1.5. Проникновение плоской электромагнитном волны в проводящую среду

Рассмотрим случай, когда плоская электромагнитная волна, распространяясь в диэлектрике, подходит нормально к плоской поверхности, ограничивающей с одной стороны проводящую среду. Допустим также, что обе среды простираются от поверхности раздела до бесконечности. Падающая волна частично отражается от поверхности проводящей среды, частично проникает в эту среду (рис. 1.5) и поглощается в ней.

Расположим оси прямоугольной системы координат, как показано на рис. 1.5. В прямоугольной системе координат ур-ния О-60) и (1.61) запишутся следующим образом:

оЕг,

(1.62)

дНу dt

д Нг dt

(1.63)

Для плоской электромагнитной волны £ и Я не зависят от

X к у (см. рис. 1.5), а только от 2 и . Поэтому - = О, - = О,

дх ду

= О, =0,Я.г. = 0. Тогда из vp-ний (1.62) X ду

лишь следующие равенства: dHu

дх (1.63)

остаются

л. -

оЕ, дНу

(1.64)

дг (-б)

Этими двумя уравнениями определяется плоская электромагнитная волна в проводящей среде.

Допустим, что напряженности магнитного и электрического полей изменяются по синусоидальному закону, т. е.

£ = £„sin(a)-f 9i),

Яу = ЯmSiп(a)<-f Фг), J где ф1 и ф2 - начальные фазы.

Представляя выражения (1.66) в показательной форме, можно написать:

р - р J (<оЧ-Ф.) р р1ф. р<<0 р J«>t

Ну = Н

I («<-)-ф,) те -

е-е" = Я™е

(1.67)