

|
|
Главная -> Радиочастотные линии 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 (3.83) Для радиочастотных кабелей при />б можно принять, что Внешний проводник коаксиального кабеля может быть биметаллическим, т. е. состоять из двух металлов. Допустим, что внутренний слой внешнего проводника имеет толщину магнитную проницаемость щ и удельное сопротивление рь Наружный слой внешнего проводника имеет соответственно параметры: /г. Мг, рг- Коэффициент экранирования биметаллического внешнего проводника коаксиального кабеля может быть определен по формуле 1 1 -бм - (3.83) Сопротивление связи коаксиального кабеля с биметаллическим внешним проводником определяется по формуле (3.84) В этих формулах kx = Y2=} соцг/рг- Ряд конструкций радиочастотных кабелей имеет внешний проводник в виде обмотки одной или несколькими металлическими лентами (плоскими проволоками). В этом случае часть тока будет проходить по винтовой линии, вследствие чего внутри трубки внешнего проводника появится продольное магнитное поле. Это поле обусловливает возникновение дополнительной индуктивности, которая отсутствует в кабелях со сплошным внешним проводником и приводит к возрастанию сопротивления связи и уменьшению экранирующей способности. Сопротивление связи коаксиального кабеля с рассматриваемым внешним проводником увеличивается также за счет небольших зазоров в спиралеобразной трубке. Небольшая доля внешнего магнитного поля, возбужденного помехонесущим током, будет проникать внутрь трубки внешнего проводника. В результате в кабельной цепи возникает напряжение, возрастающее с увеличением частоты. Поэтому сопротивление связи, начиная с некоторого определенного значения возрастающей частоты, также будет увеличиваться. Можно показать [6], что сопротивление связи кабеля со спиральным внешним проводником с углом подъема xs определяется по формуле Zss = -f [Ze -f i со Цо/4я] ctg2 Ф5, (3.85) где цо=4л-10- Г/м. В этой фор.муле Zs представляет собой сопротивление связи кабеля со сплошным внешним проводником таких же размеров, что и кабель со спиральным проводником [см. ф-лу (3.79)]. Для случая, когда >б, это сопротивление очень мало. Второй член формулы зависит от угла подъема спирали <ps и равен нулю при фз=90°. Он характеризует влияние спиралеобразной формы внешнего проводника. Сопротивление Zb является комплексным сопротивлением сплошного внешнего проводника и определяется по формуле (3.86) Угол подъема спирали фз может быть определен из следующих отношений: (3.87) А/л D = tg Bjh = cos Ф5, где h - шаг намотки спирали; В - ширина спирали. При низких частотах, когда еще не сильно сказывается.поверхностный эффект (/<б), можно положить, что Zb=Zs=Ro, т. е. где Ro - сопротивление постоянному току сплошной трубки внешнего проводника. В этом случае ф-лу (3.85) можно упростить и записать так: Z = (3.88) Первый член этой формулы учитывает удлинение пути тока вследствие спиралеобразной конструкции внешнего проводника, второй - влияние коаксиального поля. При определении экранирующих свойств коаксиального кабеля с внешним проводником из плоских проволок за ширину спирали В необходимо принимать суммарную ширину всех проволок. Формула (3.85) показывает, что сопротивление связи спиралеобразного внешнего проводника, начиная с некоторой частоты, возрастает почти пропорционально этой частоте. Поэтому коаксиальный кабель с таким внешним проводником будет плохо защищен от помех. Для повышения экранирующей способности такого кабеля внешний проводник дополнительно покрывается металлическими лентами или свинцовой оболочкой. Это обеспечивает сильное затухание осевого поля и значительное уменьшение сопротивления связи. Основная номенклатура радиочастотных кабелей имеет внешний проводник в виде оплетки, обеспечивающей необходимую гибкость кабелей при использовании их в радиотехнической аппаратуре. Теоретическое исследование экранирующих свойств оплеток представляет большие математические трудности, и пока еще нет 5-320 129 точных формул для расчета коэффициентов экранирования или сопротивления связи. Однако экспериментальные исследования в этом отношении проводились уже неоднократно. Так, Шеффер и Виман [5] измеряли сопротивление связи оплеток в диапазоне частот до 3 МГц. Роде [33, гл. IX], исследуя сопротивление связи оплеток, обнаружил, что на частотах свыше 5 МГц оно возрастает пропорционально частоте, и эта зависимость вызывается индуктивностью оплетки. Ларсен [36, гл. IX], исследуя сопротивление связи оплетки в диапазоне частот до 200 МГц, также подтвердил зависимость его от индуктивности оплетки и нашел, что величина индуктивности оплетки примерно обратно пропорциональна ее оптической плотности. Наиболее полные исследования сопротивления связи различных конструкций оплеток в спектре частот до 50 МГц проведены Крюгелем [38, гл. IX]. Измерение сопротивления связи производилось на образцах кабеля длиной 1 м с помощью измерительного устройства, схема которого приведена на рис. 9.73. Результаты измерения сопротивления связи некоторых типов кабелей с оплетками даны на рис. 3.!!. Конструктивные данные оплеток различных образцов кабелей, результаты измерений которых указаны на рис. 3.11, приведены в табл. 3.3. Таблица 3.3 Конструктивные данные оплеток 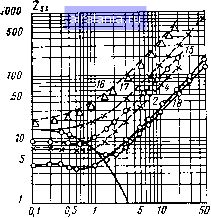 /,МГщ Рис. 3.11. Зависимость сопротивления связи Zss от частоты для некоторых оплеток из 1медных проволок диаметром 0,2 MiM
Из рис. 3.11 видно, что сопротивление связи на частотах выше 3 МГц имеет практически линейную зависимость от частоты. На низких частотах сопротивление связи примерно равно сопротивлению оплетки постоянному току. Сплошная кривая представляет сопротивление связи медной трубки без отверстий с толщиной стенки 0,2 мм. Рассмотрим один из приближенных способов расчета сопротивления связи коаксиального кабеля с оплеткой. Сопротивление связи такого кабеля можно представить следующим образом: Zss = Zs+ Zso, (3.89) где Zs - сопротивление связи внешнего проводника кабеля в виде сплошной трубки, определяемое по ф-ле (3.82); Zso - сопротивление внешнего проводника за счет отверстий в оплетке. Если принять, что на единицу длины оплетки приходится N отверстий, то сопротивление связи будет равно [6] Zso = ico- 4ЦоСвЛ (3.90) 3я{0 + 2d,) где Готв -радиус одного отверстия в оплетке. Если оплетка имеет число прядей одного направления Оь то число отверстий на длине шага h будет Ci. Тогда число отверстий на единицу длины будет N = ayh. (3.91) Определим среднюю площадь одного отверстия So, исходя из оптической плотности оплетки Р. Площадь поверхности внешнего проводника, покрытая проволоками оплетки, равна •SrtTT = Р 5„ -опл "каб» где 5каб - общая площадь поверхности изоляции кабеля. Кроме того, можно написать равенство •опл - -каб 0 отсюда So = (\-P)S,JN. Используя выражение (3.91), получим S nh(i-P){D+2di) (3.92) (3.93) (3.94) (3.95) Представляя эту площадь в виде круга с радиусом Готв, можно написать r,„=-V{l-P){D+2di)h. Подставляя это значение в ф-лу (д = 2я/, цо=4я-10-, Г/м, получаем 7 3,2.10- so- За, (Zso, Ом./м; Гц). (3.90) и имея в (3.96) виду, что (3.97) Таким образом, сопротивление связи коаксиального кабеля с оплеткой Zss. Ом/м, можно определить по формуле 3.=3+ii/(.-P)/i. (3.98) Из этой формулы видно, что при высоких частотах сопротивление связи кабеля с оплеткой прямо пропорционально частоте. Следует отметить, что оценивать экранирующие свойства радиочастотных кабелей по сопротивлению связи можно при сравнительно низких частотах (не более 200 МГц). При более высоких частотах необходимо измерять затухание экранирования. Измерения показывают, что затухание экранирования коаксиального кабеля с одной оплеткой плотностью 90±2% на частотах 1-3 ГГц имеет величину порядка 35-40 дБ. 3.6. ВЫСШИЕ ТИПЫ ВОЛН В КОАКСИАЛЬНОМ КАБЕЛЕ Высшими типами волн в коаксиальном кабеле называются электрические волны типа Е (ТМ) и магнитные волны И (ТЕ). Электрические волны типа Е характеризуются наличием продольной составляющей электрического поля Е,. Эта составляющая может быть определена из решения волнового ур-ния (1.94) с учетом наличия внутреннего проводника. Выражение для продольной составляющей электрического поля будет иметь вид = [Л, /„ (кг) + 1 (кг)] cos пере" \ (3.99) где In(kr) и Nn(kr) - функция Бесселя и Неймана п-го порядка; Л; ! В - постоянные интегрирования. Граничными условиями для рассматриваемого случая является равенство £2 = 0 при г = а и г=Ь. Используя эти условия, можно написать: AI,(ka)+BN,{ka) = OA AK{kb) + BNAkb) = Q. Из этих равенств легко получается следующее трансцендентное уравнение: ln(ka) Injkb) (3 101) Nnika) Nnikb) Отсюда следует, что каждому заданному значению п будет соответствовать бесконечное число значений кп\, кп2, кпт- Это характеризует наличие в кабеле бесконечного числа электрических волн типа Епт- Критические частоты этих воли согласно ур-нию (1.110) могут быть определены по формуле Х„р = 2я/*„„. (3.102) Корни ур-ния (3.101) могут быть определены по таблицам при-.тоже;шя 2. Минимальное значение и.меет корень при ;г = 0, т = ]. соответствующий волне типа Eoj. При этом получаем (З.ЮЭ) kQin/{b - a). (3.103) Подставляя это значение в (3.102), получим формулу для максимальной критической волны типа Е в коаксиальном кабеле Kp = 2ib-a) = D-d. (3.104) Магнитные волны типа Н характеризуются наличием продольной составляющей магнитного поля Hz. Значение этой составляющей может быть определено из решения волнового ур-ния (1.95). Для коаксиального кабеля выражение для продольной составляющей магнитного поля будет иметь вид Hz = [2In(kr) + fiaIn(kr)]cosп(р& (3.105) где A2 и B2 - постоянные интегрирования. Граничным условием в этом случае является равенство нулю д Нг производной но написать при г=а и г=Ь. Тогда из ур-ния (3.105) мож- A,rjka) + B,N{ka) = 0, A,rjkb) + B,NJkb) = 0. Решение этих уравнений относительно А2/В2 дает (3.106) (3.107) Это трансцендентное уравнение имеет бесчисленное множество корней. Некоторые из этих корней могут быть определены по таблица,м. Уравнение (3.105) показывает, что в кабеле будет бесчисленное число магнитных волн типа Нпт- Критические длины волн будут определяться по ф-ле (3.102). Самая длинная критическая волна получается при п=\ и т=1 (Нц) и определяется по формуле "кр - : л(а -f b). (3.108) Сравнивая это выражение с ф-лой (3.104), можно видеть, что наибольшей критической волной из всех волн Е и Н в коаксиальном кабеле обладает волна Нц. Следовательно, предельной частотой использования коаксиального кабеля без возникновения вол.ч высших типов является частота, определяемая по формуле /„р~- , (3.109) где с - скорость света, равная 3-10 м/с; еэкв - эквивалентная относительная диэлектрическая проницаемость диэлектрика кабеля. При подстановке в эту формулу значений диаметров D и d в миллиметрах ее можно записать следующим образом: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 0.0123 |