

|
|
Главная -> Радиочастотные линии 0 1 2 [3] 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 Подставляя эти значения в ур-ния (1.64) и (1.65) и производя сокращение на общий множитель е", получаем два уравнения: (1.68) Дифференцируя первое уравнение по е н подставляя в правую часть полученного равенства значение из второго уравнения, получаем dm, dz (1.69) Это равенство представляет собой линейное дифференциальное уравнение второго порядка с постоянным коэффициентом. Его решение имеет вид (1.70) где Al, А2 - постоянные интегрирования; (1.71) Имея в виду, что К ~yY ( + Ь выражение (1.71) можно записать так: р = = (1 + о Ущ = (I + i) Ф q = У"ыЦаа/2. (1.72) Постоянная интегрирования А2 может быть определена из следующих соображений. Если А2ФО, то с ростом z, как это видно из выражения (1.70), должна возрастать до бесконечности. Так как Нт не может расти до бесконечности при распространении волны, то, следовательно, из физических соображений должно быть Л2 = 0. Тогда Я„ = Л,e- (1.73) Постоянная Ai может быть определена, если положить z=0. В этом случае Hm=Ai, т. е. имеет заданное значение на поверхности среды. Следовательно, Ai = He"C"> =Нто- Таким образом, решение ур-ния (1.69) будет иметь следующий вид: Я„ - и то е-" sin ((О < + Фго - q). (1.74) Используя первое ур-ние (1.68), получаем следующее выражение для напряженности электрического поля: Так как -(l + i) = /e•" -qi ~iqz in/4 mo е е е СГ.75> Полученные выражения для напряженностей электрического и магнитного полей показывают, что амплитуды напряженностей по мере проникновения волны в глубь проводящей среды убывают по экспоненциальному закону. Начальная фаза колебаний изменяется пропорционально z, причем по мере проникновения в глубь среды колебания все более запаздывают по фазе по отношению к колебаниям на поверхности среды. Плотность тока изменяется по такому же закону, как и напряженность электрического поля. Следовательно, плотность тока у поверхности проводящей среды будет максимальной. У круглого-проводника плотность тока также убывает по мере удаления от поверхности в глубь проводника. Это явление называется п о -верхностным эффектом (скин-эффектом). Уравнения (1.74) и (1.75) показывают, что напряженность, электрического поля опережает по фазе напряженность магнитного поля на угол л/4. Для диэлектрика сдвиг по фазе между этими векторами равен л/2. Волновое сопротивление проводящей среды можно определить,. взяв отношение Ет к Нт- Из ур-ний (1.74) и (1.75) получим Z„ = (1.76> сопротивление проводящей среды: Следовательно, волновое имеет комплексное значение. Длина волны 1, т. е. расстояние, на котором фаза изменяется на 2л, определяется из условия qX=2n. Отсюда получаем 2 (1.77> я= = 2л1/: о г b q т ш[1оО Так как <о = 2л/, то получим 1 %2Уя- YfVaO (1.78)- Если положить, что 2=Л,, т. е. взять расстояние от поверхности проводящей среды, равное длине волны, то отношение амплитуд напряженностей полей будет равно е~"=0,00185. Это число показывает, что на весьма малом расстоянии волна практически полностью затухает. Расстояние, на котором амплитуда волны уменьшается в е раз, условно принято называть глубиной проникновения б. Ее можно определить по следующей формуле: (1.79) .Эту формулу можно записать в более удобном для практических целей виде: 100 ,/-7г- г = - У of fl. 2я a((i/(i„) 2я " (1.80) •Здесь р - удельное сопротивление, Ом.мм/м; naf/po~( - относительная магнитная проницаемость материала; / - частота, кГц; <г -удельная проводимость среды, См/м. Глубина проникновения б измеряется в миллиметрах. Кроме глубины проникновения б, характеризующей поверхностный эффект в металле, используется так называемый коэффициент вихревых токов k, 1/мм, определяемый по формуле * = >= V = -50- (размерности: р - Oim .мм/м; f - кГц). В табл. 1.1 приведены формулы определения глубины проникновения и коэффициента вихревых токов для различных металлов, а на рис. 1.6 показана зависимость величины 6 от частоты. Таблица 1.1 К определению глубины проникновения б и коэффициента вихревых токов к для различных металлов
Примечание. В таблице частота / измеряется в килогерцах. 5, ММ 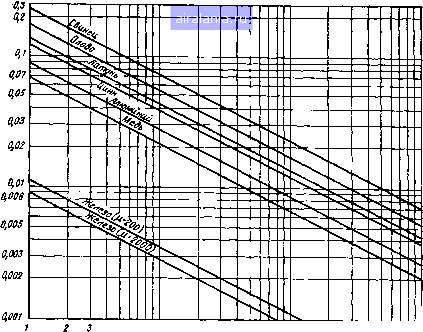 и 5 67 8910 20 30 40SO 70 100 200 300mSOO7001000 Рис. 1.6. Частотная зависимость глубины проникновения для различных металлов 1.5. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ЛИНИЯХ ПЕРЕДАЧИ Рассмотрим общие вопросы теории распространения электромагнитных волн вдоль линии передачи. Электромагнитные волны в линиях передачи распространяются вдоль каких-либо тел: однопроводных, многопроводных и коаксиальных линий, диэлектрических стержней, металлических и полупроводящих поверхностей, металлических трубок и др. Совокупность направляющих элементов образует направляющую систему - линию передачи, служащую для передачи электромагнитной волны от источника к потребителю. На рис. 1.7 представлен: ряд линий передачи, используемых на практике. Все линии передачи можно разделить на два больших класса: линии передачи открытого типа (рис. 1.7а-ё) и линии передачи закрытого типа (рис. \Лж-т). Направляемые волны делятся на поперечные электромагнитные, электрические и магнитные. Поперечными электромагнитными волнами, обозначаемыми ТЕМ, называют волны, у которых в направлении распространения отсутствуют составляющие векторов напряженностей электрического и магнитного полей (рис. 1.8). Векторы  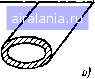   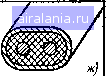  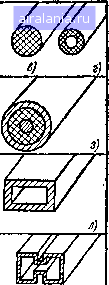 Рис, 1.7. Основные виды направляющих линий: а) двухпроводная яеэкранированная линия; б) однопроводная линия поверхностной волны; S, г) «еэкранированиые круглые сплошной и трубчатый соответственно диэлектрические волноводы; д, г) «еэкранированные диэлектрические волноводы эллиптический и прямоугольный соответственно; ж) двухпроводная симметричная экранированная линия; з) коаксиальная линия; и, к, л) эллиптический, круглый и прямоугольный волноводы; м,н,о) экранированные диэлектрические волноводы (круглый сплошной, трубчатый, прямоугольный); п) Н-образный волновод; р,с,т) полосковые линии  ff-ff, (Мг=0) Е=Ед HanpaS/ieHue распространения Рис. 1.8. Распространение поперечной электромагнитной волны типа ТЕМ напряженностей электрического и магнитного полей ТЕМ волн находятся в плоскости, перпендикулярной направлению распространения. К числу волн типа ТЕМ относятся волны в свободном пространстве, а также волны основного типа в двухпроводных и коаксиальных линиях. Электрическими волнами, обозначаемыми Е, называют волны, у которых вектор напряженности магнитного поля имеет только поперечную составляющую, а вектор напряженностРЕ электрического поля, помимо поперечной, имеет также продольную составляющую, т. е. составляющую в направлении распространения волны (рис. 1.9). Эти волны называют иногда поперечно-магнитными волнами. 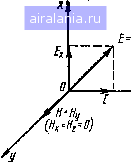 (Еу-0) ИапраВлте распространения  tiz Z Направление распространения Рис. 1.9. Распространение эле«трнче- Рис. 1,10. Распространение магнитной ской волны типа Е волны типа Н Магнитными волнами, обозначаемыми Н, называют волны, у которых вектор напряженности электрического поля имеет только поперечную составляющую, а вектор напряженности магнитного поля - как поперечную, так и продольную составляющие (рис. 1.10). Магнитные волны называют иногда поперечно-электрическими волнами. При изучении распространения направляемых волн удобно направить ось Z вдоль оси линии передачи энергии. В этом случае составляющие Ег и Нг как в прямоугольной, так и в цилиндрической системах координат удовлетворяют волновому уравнению. Определяя £- и Нг непосредственно из волновых уравнений, можно выразить через них остальные составляющие, используя шесть уравнений Максвелла в скалярной форме. Допустим, что все составляющие поля в направлении координаты Z изменяются по экспоненциальному закону, т. е. Л = Лое- (1.81> где А - любая составляющая вектора Е или Я; Ло - начальная составляющая вектора Е или Я; у - коэффициент распространения. Первая и вторая производные любой из составляющих по координате Z равны: дг дг = -уАе = -уЛ, (1.82> (1.83) 25 0 1 2 [3] 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 0.0116 |