

|
|
Главная -> Радиочастотные линии 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 [35] 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 18г-1-1-1-1-1 учитывающие влияние поверхност- Ч д ного эффекта и эффекта близости, зна- !А ----- чения которых приведены в табл. 2.1, v. а 9 и & - коэффициенты, введенные и f/0---==5 табулированные Бэттервортсом, кото- рые при низких частотах стремятся к Лхт"--- единице, а при высоких зависят от плотности намотки, как указано на gp I I I I I рис. 5.2. 10 0,8 0,6 0, ОЛ о Пользуясь этими кривыми и дан- ными последней строки табл. 2.1, по- Рис. 5.2. Эиачеиия коэффициен- "У ВЫСОКИХ частот Ом/м, тов 9 и д для расчета актив- Равное иого сопротивления спирали Г + 1 + -V 3 1-f 6 + d (5.23) 15 d )obf По:следнее приближение (справедливо лри условии dtl3, которое выполняется практически всегда. Та.мим образом, для кабеля со спиралью из круглой проволоКи можно иепосредственно пользоваться ф-лами (5.20) и (5.21), лишь заменив в первой из них пЬ на 3-\-2t/5d. Дифференцируя (5.23) по d и приравнивая производную нулю, получаем оптимальный днам.етр проволоки спирали d = ]/"- W, соответствующий минимуму потерь. Этот минимум выражен слабо. Активное сопротивление коаксиального кабеля с незамкнутым экраном R, Ом/м, также определяется выражениями (5.20) - (5.23), если в первой из них положить В-оо, т. е. отбросить поправку, обусловленную экранирующим .действием .внешнего проводника [3]. Так, для спирали из круглой проволоки /З b + d j J b (5.24) я (6 + 2d) я D Сопротивление симметричного кабеля с общим сердечником Rz, Ом/.м, связанное с продольны.м магнитным поле.м, рассчитывается по ф-лам (5.20) и (5.23), если учесть те же поправки на суммирование продольных магнитных полей обоих проводников и на овальность витков из-за частых пересечений, которые учитывались при выводе ф-лы (5.10). Так как в симметричных кабелях используются только круглые проволоки я немагнитные материалы, то ?,= 12fl -f b + 1 ,Ы \5dl abi (02 4d (6+ l,5d)]2 " -"l Вторая (Составляющая активного сопропивления /?ф, Ом/м, связанная с продольными токами, равна R----. (5.26) * яаб (& + 1,5d-f rf) В этой формуле не учтены потери в экране; они ничтожны, так как поперечные магиипные !ПОЛя от обоих проводников практически компенсируются. Наконец, для симметричного кабеля с параллельными сердечниками .сопротивления .обоих .спиральных проводников складываются, а влияние экрана на Rz отсутствует: b + d Rz=a I 15 d i (5.27) Составляющая , Ом/м, .определяется по ф-ле (6.25) для симметричного экранирова.нного кабеля: .Ф - яаб(6+2) (b+2d)2 8К2 Dc яаб D*-с* (5.28) Вторичные параметры. Зная емкость, индуктивность и активное .сопротивление (спирального кабеля, а та(кже tg6 его изоляции, можно получить вторичные параметры кабеля, пользуясь обычными формула.м1и для (коэффициента затухания а, дБ/м: a = a+a = 4,325{RVQL+ (oVTCtgd), коэффициента фазы р, рад/м: й) ? гт7 f ас (5.29) (5.30) (второй член в скобках определяет зав.исидш.сть .задерж.ки от частоты; он представляет интерес только .при низких частотах) (и волнового (сопротивления Zb, Ом: (5.31) - «й Иногда .коэффициент затухания относят (Не к единице длины, а к единице времени задержки. В этом (Случае его обычно выражают в дБ/мкс ,и определяют по формуле а - = 4,325 (R/L + а tg6). (5.32) Т р Радиочастотные кабели, в частности кабели задержки, удобно характеризовать также величиной добротности, как любой элемент радиосхемы: озЮТ (nL (йТ р R + GZl (5.33) где W -энергия поля и Р -средняя мощнОСть потерь иа едини- це длины кабеля. Очевидно, что добротность есть величина, обратная а/Т. Точные выражения для юторичных параметров спиралыных кабелей довольно громоздки; здесь будут приведены лишь сугубо приближенные формулы, удобные для .сравнения т оценки кабелей разных типов. Будем полагать, как это ;и бьшает .обычно, что сердечник и изоляция выполиены мз иолиэтилена (82,3; tg(5<5-10-*), а .п.роводии.ки -из круглой медной (проволоки; шаг сп1Ирал;и м/ного (М€.ньше диаметра сердечника. Выразим все размеры в миллиметрах, а частоту--в мегагерцах. Тогда для коаксиального кабеля с замкнутым экраном и KiS воЛН.о,вое (сопротивление Zb, Ом, будет равно 90 4 Y[D~iWdf] In ,-2d . коэффициент укорочения длины в.олны 26!п- b+2d a отношение а/Т, дБ/мкс, « 43,2 vf Для (коаксиального кабеля с «езам(Юнутым экраном (5.34а) (5.346) (5.34b) Z. 125 , J 2,44. /» . 3„ yj- Для .шм.метр,,„ного кабгля ,с общи» сердеммам "(К.хЗ) 7 ~ 125---- "- F?r у (I+ld-dnD-ib+lSd+dr Arch -L , t 1° i/------ I ЪТТГ F( + 1.5d-№M&+1.5d+d)j/Arch. I (5 36) « 952Z) Arch i/2d имс5Г "P"«°™ «беля ,c .параллельными сердечниками 52ln D2 + c2 > a 38,9 , r~ T h У (5.37) Расчет .мощности, которая может длительно передаваться по коаксиальному кабелю -с замкнутым экрано(М в режиме согасо ваянной нагрузки, производится обычным образом n™e(S°. Приближенная формула для Р, кВт, имеет вид 1 - 4 92« {5.38} где манс - ма(Ксимальная длительно допускаемая темнература изоляции, °С; - температура окружающего воздуха, °С. Остальные типы (Спиральных ка(белей для передачи большой .мощности не используются. 5.3. ВЫБОР КОНСТРУКЦИИ СПИРАЛЬНОГО КАБЕЛЯ При (КОН(Струиро1вании апиральных кабелей н.еобходим.о учитывать .существ.аБан1ие некоторых со.отношений между осно1вными размера(М(и кабеля, (обеспечивающих оптимальные электрические хара,ктеристи(К1и. Эти ооотношения за.ансят от типа (кабеля и от предъявляемых требований. Так, в вы1СО(Коомных кабелях обычно требуется получить (наименьшее затухание .на единицу длины при дан1ных 1волн101вом сО(противлении и диаметре по изоляции. Здесь мин1имуму затуха!Н,ия (соответствует ми.нимум активного .сопротив-ления. Рассмотр:И1М кабель с замк/нутым экраном. Выразив шаг t через Zj,, D, b и d с помощью ф-л (5.6) и (5.13), подставив его значение в (5.20), продифференцировав по Ь и приравняв производную нулю, легко получить уравнение, определяющее оптималь.ное отношение b/D. При этом оказы,вается, что это .о-тношение (Сйвер-шенно не зависит от Z„, / и D и лишь немного от d /и К2. В предельном случае d=0, /(2=1, (6 ))опт= 1/е. В общем .случае решение предста1влено на рис. 5.3а в виде семейства кривых. 0,3 0,1
0,01 0,06 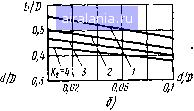 Рис. 5.3. Оптимальное отношение bjD для коаксиальных кабелей с замк1нутым экраном: а) высокоомиые кабели; б) кабели задержки При указа,н.ном вы(боре размеров .коэффициент затухания а, дБ/м, кабеля .со .спиралью .из круглой 1п:ро(3олоки и изоляцией из полиэтилена может (Приближенно вычисляться по формуле (/СгЛЗ) a.68,5-10--VT (5.39) Для спирали из (тьтоской проволоюи коэффициент 0,08 следует за- менить на 0,07. Здесь и далее коэффициент затухания выражается через b noTOiMy, что в (ГОСТ 11326.0-71 величина диаметра серд ечниК а (Стан д а р ти зова н а. Наибольшее волновое (сопротивление, которое (Может быть достигнуто (При данных диаметре но нэолации т шаге ;сп;ирали. :32-5--90- (5.40) получается (при ft/D = 0,48. Аналопично для (кабелей задерж(Ки, (где спремятся получить наи.меньшее ,затуха(Ние (на ед/иницу времени :зад(ержК(И при дан1ных водноBO..M сопротивлении и диаметре (по изоляции, можно получить свое оптимальное отношение bjD, представленное кривыми на рис. 5.36. При это(М (коэффициент затухания, волно(Вое сопротивление 1и в(ремя задержки определяются .следующими фор.му-лами: 0,54 Тл 0,012 - (5.41) (а/Г, дБ/мкс; Zb, Ом; Г, MiKc/m). Наличие минимума потерь ib спиральных кабелях с замкнутым экранам связано (с тем, что, как говор.илось выше, ток в них течет параллельно и по внутренней и по внешней СторО(нам .спирального проводника, тогда как в отсутств1ие экрана (или (при (неза.мк-нутйм экране) он течет только ио (внутренией стороне. Чем экран ближе, т. е. чем bjD больше, тем большая доля тока ответвляется на (Внешнюю сторону, в связи с чем (до шекоторого предела) потеря в спирали уменьшаются. Одно1временио потери в экране увеличп-заются. Оптимальное значение bjD достигается, когда уменьшение потерь в спирали ко.мпенсируется их увеличением в экране. Отсюда hciho, что для кабелей с незамкнутым экраном оптимальных (соотношений между размерами не существует. Для предварительного расчета и выбора возможных вариантов таких кабеле!! удобно пользоваться Н0(мограммой (4], приведенной на рис. 5.4. Но.мограмма составлена для случаев 6 = 7 мм (стандар-тизО(ва1.чный диаметр .сердечника, пр.именяе.мый во всех отечественных кабелях этого типа) и рс = 1. На номограм.ме по оси абсцисс отложена величина задержки, по .оси ординат -волно.в.ое .сопротивление; .сетка .показывает основные характеристики (емкость, индуктивность, шаг 1на,мотки) кабеля с заданными Т и Zb. Из но.мограммы (видно, какие значения Т .и Zb мо,гут быть одновременно 1реализова(ны .на практике. Наклонная прямая С=2 нФ/м (наибольшая емкость, достижимая при Ь = 7 м.м), ограничивающая область допустимых значений снизу, показы.ва.ет м(И1Нимальное во-лновое .00(П.ротивление, (когорое может .иметь кабель с заданной задержкой, а гипербола L = = 3000 ..мкГ/м, огра(Ничивающая эту область (оверху, указывает соответствующее макаимальное сопротивление (при .иамотке эмалированной проволокой d=0,l мм, /=0,13 (мм). жашим яа погращ.11чяых линиях С = 2.нФ;>1 « L-mx «и л». 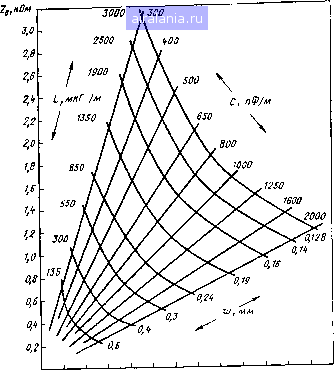 Т,мнс/м 0,2 0,6 0,8 1,0 1,2 1,1 1,6 1,8 2,0 2,2 7 2,В Рис. 5.4. Номограм.ча для расчета кабелей задержки с сердеч-нико.м диаметром 7 мм н незамкнутым экраном Если диаметр сердеч.ника 6=77 мм и цс>1, структура номограммы .сохраняется, (Но максимальная индуктивность увел.ичива-ется в рс6/49 раз, а ма.ксимальная ем.кость в b раз; цифры на шкале / долж.ны быть увел(ичены в Y УсП раз. При 1Конструирова.ии,и симметрич.ных спиральных кабелей с общим сердечнико.м также можно пользоваться оптимальными соотношениями, вы1в.еде1нными для .коаксиальных кабелей и изображенными (на рис. 5.3а. Однако ф-лы (5.39) - (5.40) здесь непрнме-НИ.МЫ. Замети.м еще, что, поскольку симметричные .кабел1И используются глав.ным .образом в высо.кочастотных трактах, от них требуется высокая степень однородности, т. с. постоянство .волно(вого сопротивлешш .по длине. Из ф-лы (5.36) видно, что 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 [35] 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 0.0125 |