Выразим составляющие поля через Ег и s прямоугольной системе координат. Используя ур-ния (1.16), (1.17), (1.82) и 0-83), можно получить:

1 /

дх ду

Е =-

дЕг , ; дНг

у2 +

-- (-

дЕг \

- Y + 10)6

/ , . ,дЕг

(1.84) (1.85) (1.86) (1.87)

ду аж .

Для цилиндрической системы координат из ур-ний (1.201 (1.21), (1.82) и (1.83) получим:

Е, =--

.0=--

0)2 (

Значения Е и Я определяются путем решения волновых уравнений. В соответствии с выражением (1.32) волновое уравнение в прямоугольной системе координат для составляющей Ег. будет

дЕг , дЕг jdEz

+ coVae = 0.

дх ду дг Используя выражение (1.83), можно написать

(1.92)

дх ду

где k = yf- + ViaS.iii\

Аналогично для составляющей Нг волновое уравнение будет

(1.93)

Волновые уравнения в цилиндрической системе координат для Я, и £г в соответствии с ур-ниями (1.32), (1.35), (1.27) и (1.83) будут следующими:

дЕ. , , .Я. , , дЕ. . „

(1.95)

дг d4h дг

I дЕг 1 дЕг

+ \ + кИгО.

Используя полученные равенства для различных составляющих поля, устанавливаем некоторые важные соотношения для волн типов ТЕМ, Е и Н.

Для волн типа ТЕМ, у которых Ez~Hz=0, следует принять

Y* + liaeV = 0. (1.96)

Отсюда коэффициент распространения

y=±iaVW- (1.97)

Подставив в эту формулу значение е из выражения (1.15), получим

= ±1со/

шва/

(1.98>

Тогда коэффициент затухания а и коэффициент фазы р будут равны:

/(1/

(1.99> (1.100)

В случае, если среда не обладает проводимостью, а=0,. и тогда

а = О, = а)е„, у = ± i р. (1.101>

Из этих уравнений видно, что коэффициент распространения является мнимой величиной и, следовательно, распространение волны происходит без затухания.

Волновое сопротивление, определяемое как отношение напряженности электрического поля к напряженности магнитного поля, для волн типа ТЕМ будет равно

ТЕМ = (1-102)

Это выражение получается из ф-л (1.16) и (1.17), если учесть, что Я2=£г=0, и выражения (1.82). Для среды без потерь

ZTEM = Kiu = - (1-I03)

Волновые ур-ния (1.24) и (1.25) для волн типа ТЕМ с учетом выражений (1.83) и (1.96) примут вид

дх дН

ду дН

= 0.

(I.I04) (1.105)

ду ду

Эти уравнения характеризуют геометрическую структуру поля волн типа ТЕМ. В ф-лы (1.104) и (1.105) не входит частота, сле-

довательно, структура поля волн типа ТЕМ не зависит от частоты, т. е. волны ТЕМ не обладают дисперсией.

При неидеальной проводимости металлических проводников коаксиальной линии электромагнитное поле проникает в металл. В соответствии с граничными условиями Леонтовича-Щукина появляется отличная от нуля касательная составляющая электрического поля, параллельная оси z, и, кроме волны ТЕМ, возникают волны высших типов.

Для электрических волн Е и магнитных волн И волновые уравнения выражаются соответственно ф-лами (1.92) и (1.93). Предположим для этих случаев, что среда, в которой распространяются волны, не обладает проводимостью и ъ=Ъа- Тогда можно написать, что

-с =

выражение

Имея в виду, что й) = 2я/= -

можно записать так:

A* = Y* + (2A)* = V* + pl Отсюда коэффициент распространения будет равен

(1.106) (1.106)

(1.107) (1.108)

Из этой формулы видно, что при >р(р = 2лА=2л с) коэффициент распространения является вещественной величиной, поле в направлении z затухает и энергия распространяется. При fe<p величина у является мнимой величиной и энергия распространяется без затухания. Случай k- = 2n/X = 2nf/c является критическим, при котором Y = 0- Частота, соответствующая этому случаю, называется критической и определяется из выражения

(1.109)

t

/ кр 7Г~ -

2я 2п IBofla

критическая длина волны 2я 2яс

, с 2Я 2ЯС 1/--

(1.110)

Отсюда вытекает одна из основных особенностей волн типов Е и Н. Эти волны, в отличие от волн типа ТЕМ, могут распространяться, только начиная с некоторой определенной критической частоты. Область волн ХЖр и частот /</кр является областью отсечки, в которой линия не может быть использована для обычной передачи энергии.

Первым высшим типом волн в коаксиальной линии является волна Ни. Структура этой волны в поперечном сечении линии показана на рис. 1.11. Если радиус внутреннего проводника в коаксиальной линии равен нулю (проводник отсутствует), коаксиальная линия превращается в круглый волновод, низшим типом волны в котором является волна Нц. Введение тонкого внутреннего про-

28

водника слабо влияет на распространение волны Нц из-за отсутствия у нее продольных составляющих элек-трачеокого поля. Повтому при малых значениях (внутреннего проводника длина волны Нц В (Коаксиальной линии приближенно равна критической длине волны Нц IB круглом ,волно1воде.

Подставив в ф-лу (1.108) значение из ф-лы (1.109) и имея в виду, что Р=!2лД, получи(м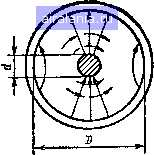

1 = 1Р/1-

=1Р/-{YJ- -

Рис. 1.11. Структура волны типа Ни в поперечном сечении коаксиальной линии

Определим волновое сопротивление для волн типа Е. Волновым сопротивлением в этом случае называют отношение поперечной составляющей вектора напряженности электрического поля к поперечной составляющей вектора напряженности магнитного поля. Для волн типа Е (Яг=0) ур-ния (1.84) -(1.87) запишутся так:

£. = -

£, = -Я„:

дх дЕг

i сое дЕ,

Y-4-(iueu)2

i (08

Y Ч- Цавш

Подставив в (1.112) <1.114) и (1.115), получим

dEz дх

(1.112) (1.113) (1.114) (1.115)

и (1.113) значения

дЕг дх

дЕ ду

Используя эти выражения, получим следующую волнового сопротивления:

1 ше

(1.116) (1.117)

формулу для

(1.118)

Для случая","когда среда, в которое распространяются волНы, не обладает проводимостью, ф-ла (1.118) примет вид

ZE=V/icue„. (1.119)

Подставляя в эту формулу значения © и у из ф-л (1.101) и (1.111) и используя выражение (1.103), получаем

- ТЕМ

Анализ этой формулы показывает, что волновое сопротивление волн типа Е в области частот выше критической меньше волнового сопротивления волн типа ТЕМ. При увеличении частоты до бесконечности волновое сопротивление увеличивается, стремясь к Ztem • При /=/кр волновое сопротивление равно нулю.

Определим волновое сопротивление для волн типа Н. Для этого типа волн £=0 и ур-ния (1.84) -(1.87) запишутся так:

(1.121) (1.122) (1.123) (1.124)

из (1.123)

у дНг

Y-fHaetu дх

Y дНг

Y-ftiflSw ду

Подставив в (1.121) и (1.122) значения и

и (1.124), получим

(1.125) (1.126)

Используя эти выражения, получим следующую формулу для волнового сопротивления волн типа Н:

2н =

(1.127)

Подставляя в эту формулу значения m и у из ф-л (1.101) и (1.111) и используя выражение (1.103), получаем

(1.128)

Рнс. 1.12. Завнсн.мость волнового сопротивления волн типов ТЕМ, Е н Н от частоты

Отсюда видно, что волновое сопротивление волн типа Н при возрастании частоты выше критической уменьшается, оставаясь, однако, все время выше волнового сопротивления волн типа ТЕМ. При увеличении частоты до бесконечности волновое сопротивление волн типа Н стремится к Ztem. При /=/кр волновое сопротивление волн типа И стремится к бес-? конечности. На рис. 1.12 показано изменение волнового сопротивления волн типов Е, Н и ТЕМ от частоты.

1.6. ФАЗОВАЯ И ГРУППОВАЯ СКОРОСТИ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

Решение волновых ур-ний (1.92) и (1.93) приводит к следующим общим выражениям электрического и магнитного полей в линии:

Ш-Уг

.Ш-Уг

(1.129) (1.130)

Имея в виду, что коэффициент распространения у=а+1р, можно написать:

,i (<в/-Pz) -az

Нг=Нт{х, y)e"•--Pe-"

(1.131) (1.132)

Отсюда видно, что при чисто мнимой величине у(а = 0) волна распространяется вдоль линии без затухания. При чисто действительной величине у(Р = 0) волна не распространяется и поле затухает вдоль оси 2 по экспоненциальному закону без сдвига по фазе.

Фазовой скоростью называется скорость, с которой распространяется в линии состояние равной фазы волны, например, скорость, с которой перемещается вдоль линии некоторый максимум напряжения или тока.

Условие постоянства фазы волны, как это следует из ур-ний (1.131) и (1.132), можно записать в виде равенства Ш-р2= = const. Дифференцируя обе части этого равенства по переменно-

му t, получаем ш = pd2, - =

рость определяется уравнением Уф = й)/р.

. Таким образом, фазовая ско-

(1.133)