Если длина волны в рассматриваемой передающей линии К, то

р = 2л/Я (1.134)

является волновым числом, показывающим, сколько длин волн содержится в отрезке данной линии длиной 2л. Подставив это значение в ф-лу (1.133), получим

Vф = (aЩn. (1.135)

Для случая волн типа ТЕМ, принимая а=0 (среда, не обладающая проводимостью), из ф-лы (1.100) можно написать

p = aKiw (1.136)

Используя это равенство, можно записать ф-лу (1.133) так:

гФ= VVeHa. (1.137)

Обозначая относительные диэлектрическую и магнитную проницаемости е и fi, ф-лу (1.137) можно записать иначе:

Оф = с/Уцй (1.138)

где с - скорость света в вакууме. Для свободного пространства е = л=1 и фазовая скорость волны равна скорости света и не зависит от частоты.

Для волн типов Е и И коэффициент распространения определяется выражением (1.108). Подставив в эту формулу значение из выражения (1.110), легко можно найти, что

Y = ipKl-(VA.„p)= ipKl-(/„p )l (1.139)

Из этого выражения следует, что для частот выше критической фазовый множитель для волн типов Е и И

рф = Р К1 - i/K,f = Р1/1 - (Ш. (1.140)

Подставив это значение в ф-лу (1.133), получим следующее выражение для фазовой скорости волн типов Е и И:

(1.141)

Данное выражение показывает, что фазовая скорость волн типов Е и И всегда больше или в пределе равна скорости света. Фазовая скорость зависит от частоты и указывает на наличие дисперсии в этих передающих линиях.

Дисперсией называется зависимость фазовой скорости от частоты. Волны, для которых имеет место дисперсия, называются диспергирующими. Волна типа ТЕМ будет недиспергирую-щей, если параметры среды Ва и Ца не зависят от частоты. Зависимость фазовой скорости от частоты ( /кр) для различных типов волн показана на рис. 1.13.

Понятие фазовой скорости относится лишь к режиму установившихся гармонических колебаний. По линиям же могут передаваться сигналы, которые можно представить в виде совокупнос-

Рнс. 1.13. Зависимость фазовой скорости от частоты для различных типов воля

ти бесконечно большого числа гармонических со- ставляющих. Фазовые скорости этих составляющих, различных по частоте, могут быть различны- ми. В этом случае для характеристики скорости распространения сигнала недостаточно понятия фазовой скорости, и поэтому (Ч вводится понятие групповой скорости.

Групповая скорость определяет скорость распространения максимума огибающей группы смежных по частоте составляющих сложного колебания. Она характеризует, таким образом, скорость, с которой распространяется максимум энергии группы волн, частоты которых ограничены некоторой узкой полосой.

Выведем формулу, связывающую групповую скорость с параметрами линии передачи. Рассмотрим два колебания с близко расположенными частотами, входящими в спектр амплитудномо-дулированного сигнала. В соответствии с выражениями (1.129) и (1.130) эти два колебания, распространяющиеся в направлении оси Z, в общем случае можно представить так:

Л, = Л1„е"-Ч (1.142)

Л, = Л2„е--Ч (1.143)

Суммарное поле этих двух колебаний, если принять для упрощения Л1т = Л2т = Лт, буДеТ

Л = Л„е-

(1.144)

Аа) = со2 -Ml, (1.145)

Ay = Y2 Yi. (1.146)

Положим для упрощения, что волны распространяются без затухания и Y=i р. Тогда ур-ние (1.144) примет вид

Л = Л„е"---М1+е""-")- (Г.147)

Анализ этого выражения показывает, что в линии будет иметь

2Л„ COS

место волна, амплитуда которой, равная л (если Ap<Pi и Aoj-Ccdi), медленно изменяется от точки к точке

2-320

линии между значениями 2Ат и нулем. Таким образом, по линии перемещается волновой пакет, огибающая которого изменяется по закону изменения амплитуды [см. (1.147)]. ,

Условием постоянства фиксированной точки огибающей ампли-тудномодулированного сигнала, например максимального значения, будет следующее равенство:

Аш - Ар Z = const. (1.148)

Дифференцируя это выражение, как и при определении фазовой скорости, получаем

Aoadt - Af)dz = 0. (1.149)

Отсюда скорость распространения максимума огибающей, т. е. групповая скорость, будет равна

= dz/d = Аш/Др. (1.150)

Если рассматривать непрерывный частотный спектр модулированного колебания, то в пределе можно написать

v = daldf>. (1.151)

Эта формула показывает, что групповая скорость волн, распространяющихся по линии, в общем случае не совпадает с фазовой скоростью. Если произвести замену переменных i) = pVф и р - 2п/к, то можно установить связь между групповой скоростью Угр, фазовой скоростью Vф и длиной волны X. Произведя простые преобразования, можно написать

При е = \1=1 эта формула примет вид

= V - k

(1.152)

Определим выражения групповой скорости для различных типов волн.

Для волн типа ТЕМ при а=0, т. е. для среды, не обладающей проводимостью, групповую скорость определим из ф-лы (1.136): ы.= р (Хаба . Используя ДЛЯ ЭТОГО выражвния ф-лу (1.151), получаем

= VWJa = с/Кце. (1.153)

Сравнивая это выражение с ф-лой (1.137), видим, что групповая скорость для пространства, не ограниченного проводниками, равна фазовой скорости. Произведение фазовой и групповой скоростей для пространства, не обладающего проводимостью, равно

гр1ф= 1/11ае« = с>11. (1.154)

Если е = (х=1, то произведение фазовой и групповой скоростей равно квадрату скорости света.

Для волн типов Е и И групповая скорость определяется по формуле

гр =

(1.155)

V,, = с 1/1-(ЯА„/ = сУ\~ (fjff.

( 1.156)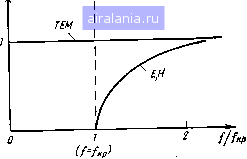

Рис. 1.14, Зависимость групповой скорости от частоты для различных типов волн

Как видно, групповая скорость всегда меньше скорости света. При увеличении частоты групповая скорость возрастает, стремясь к скорости света при частоте, стремящейся к Р бесконечности. При / = =/кр групповая скорость равна нулю. Это значит, что на частоте /кр энергия в направлении оси z не распространяется.

График изменения групповой скорости в зависимости от частоты приведен на рис. 1.14.

Произведение фазовой и групповой скоростей для волн типов Е и И, как следует из ур-ний (1.156) и (1.141), так же

как и для волн типа ТЕМ, равно квадрату скорости света.

Возможно распространение электромагнитной энергии в линии передачи не в одном, а в нескольких направлениях: а) параллельно оси г, б) по кривым линиям при общем поступательном дви-же !ии1 вдоль оси z (рис. 1.15) [37]. В первом случае векторы Е и И должны находиться в плоскости, перпендикулярной ос и 2, т. е. имеет место волна типа ТЕМ. Во втором случае векторы Е и ЬГдолжнь! находиться в плоскостях, перпендикулярных соответствующим участкам кривой линии, и, следовательно, хотя бы один из векторов напряженностей электромагнитного поля (Е н И) имеет продольную составляющую. В данном случае вдоль оси z распространяются олнь1 типа Е или Н.

При передаче Е и И волн парциальная ТЕМ волна распространяется под углом <р к оси 2 (рис. 1.15d).

Фронт волны ТЕМ перпендикулярен оси Zi и перемещается в направлении этой оси с фазовой скоростью, равной скорости света в среде: Vo=l/VBaVia = >-/T, где Г - период колебаний. За время, равное периоду колебаний, фронт волны ТЕМ переместится вдоль оси 21 на расстояние к (расстояние 1-2 на рис. 1.15d). Путь, пройденный за то же время фронтом волны вдоль оси z, будет больше {1-2)\ соответственно длина волны, распространяющейся вдоль оси 2, также больше и равна Л = >/cosф. Фазо вая скорость по оси 2 равна и,, = Л/7 = Uo/cos ф, т. е. фазовая скорость волн Е и И всегда превышает скорость света в среде. 2* 35

Возникновение волн типов Е и Н возможно в неоднородной среде, на границе раздела двух сред и т. д. В этих случаях распространяющееся электромагнитное поле может быть представлено в виде суперпозиции парциальных волн ТЕМ, совершающих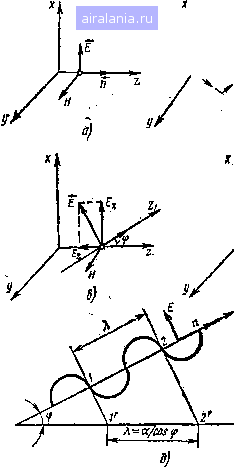

Рис. 1.15. Различные направления распространения электромагнитной энергии;

а) волна ТЕМ - параллельна оси z; о) волна ТЕМ - под углом к оси г; в) волна Е -под углом к оси г; г) волна Н -под углом к оси г; д) парциальная ТЕМ волна -под углом <р к оси Z

«скачки» между обращающими поверхностями. Причем в общем случае волны Е и Н могут представлять собой суперпозицию многих парциальных волн ТЕМ, одновременно распространяющихся под различными углами.

1.7. ПОЛНОЕ СОПРОТИВЛЕНИЕ ОДИНОЧНОГО ПРОВОДНИКА

Используя основные уравнения электромагнитного поля, можно определить полное внутреннее сопротивление одиночного проводника, которое необходимо знать при расчете параметров радиочастотных кабелей и других линий передачи.

Примем, что цилиндрический проводник радиусом а имеет удельное сопротивление р и магнитную проницаемость a. Напряженности магнитного и электрического полей в проводнике связаны между собой ур-ниями (1.60) и (1.61). В цилиндрической системе координат эти уравнения можно представить выражениями:

Я„ I дЕг .

дг 1

dEz d(f

--2- = - i 0)Цо

дЕг дЕг

дг дН.

дг дНг

дг Н.

(1.157)

Ez Р

гЗф дНг

dHz ~дГ

1. -

(I.I58)

Так как внутри проводника токи текут только в направлении оси проводника, принимаемой нами за ось z, то в ур-ниях (1.157) и (1.158) следует учитывать лишь три составляющие: Е, Нг и Н ; остальные составляющие будут равны нулю.

Подставив в ур-ния (1.157) и (1.158) £г=0, =0 и Яг=0, получим:

Нг = -:

i Wfia г а ф

1 дЕг

1 (Ща

дг 1

г г Зф

(1.159) (1.160) (1.161)

Производя дифференцирование и соответствующую подстановку в ур-ние (1.161), получаем

SEt , \ dEz , 1 дЕг

дг"

= ikE„

(1.162)

где =l/(ofia/p - коэффициент вихревых токов.

Так как одиночный цилиндрический проводник имеет осевую симметрию, то частные производные относительно касательной к