При попарной перестановке модулей Ei и Ej суммарная длина связей их со всеми остальными модулями станет равна

1(-.-)=2(г,л,-,+ол,,).

(1.5)

<=1

Таким образом, можно вычислить изменение суммарной длины связей модулей Е и Ej со всеми остальными, полученное при их перестановке:

д(-.Л (.7) (Л0 2г,Д,,-2(г,,-г,)(/С,.,-/С,,). (1.6)

По формуле (1.6) вычисляется матрица приращений для всех попарных перестановок, на основании анализа которой и производятся перемещения модулей иа ллате.

Рассмотрим структурную схему алгоритма (рис. 1.14).

1. Вычисление матрицы расстояний между точками на плате, в которых размещаются модули

21

. . .Г

23 • • - in nz nn

(1.7)

Эта матрица вычисляется один раз и действительна для всех циклов алгоритма.

Очевидно, что Гц =/22= - . =Vnn=0.

2. Составление матрицы связей между модулями. Элемент матрицы Ki] численно равен количеству проводников, соединяющих контакты модулей Е{ и Ej.

Матрица связей составляется для каждого цикла алгоритма. В первом цикле используютСя данные матрицы связей начального размещения модулей Ко, во втором цикле работы алгоритма в матрицу Kl занесены результаты перестановок, вычисленных в первом цикле и т. д.

3. Вычисление элементов матрицы приращений суммарной длины всех связей производится по формуле (1.6) для всех возможных попарных перестановок.

Вычисление

матрицы расстояний

2 Составление матрицы связей между модулями.

Вычисление матрицы „ приращении

суммарной длины Всех сВязей

Проверка наличия отрицательных элементов В матрице приращения

Выделение подмножества попарных перемещении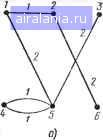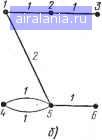

Рис. 1.15. Первоначальное размещение модулей и расстояний между точками на плате, представленное в виде графа (а); полученное после первого цикла алгоритма в виде графа (б)

6 Вывод

результатов решения задачи размещения

Рис. 1.14. Структурная схема алгоритма последовательной оптимизации размещения узлов на плате с помощью групповой перестановки

4. Блок 4 алгоритма проверяет наличие отрицательных элементов IB матрице приращений, что означает возможность оптимизации имеющегося «а плате размещения модулей. В случае, если отрицательных элементов нет, т. е любая перестановка модулей приводит к увеличению суммарной длины всех связей, то результат размещения, полученный в предыдущем цикле алгоритма, является окончательным.

5. Если условие 4 выполняется, то проводится анализ всего множества отрицательных элементов матрицы приращений и выделение подмножества элементов, соответствующих попарным перемещениям, которые удовлетворяют рассмотренным ранее требованиям. .

Попарные перемещения производятся по индексам выделенных элементов матрицы приращений .и учитываются при составлений в следующем цикле алгоритма матрицы связей между модулями.

Проиллюстрируем работу алгоритма следующим простым примером решения задачи размещения шести модулей.

Пусть начальное размещение модулей и геометрические расстояния между точками, в которых они размещаются, характеризуются матрицами Rk Ко

> 0 =

Такое размещение можно представить в виде графа (рис. 1.15, а), вершины которого соответствуют модулям, а ребра - связям между ними Lo=9.

По формуле (1.7) вычисляется матрица приращений суммарной длины всех связей при попарных перестановках модулей:

Ап =

Отрицательными являются элементы AL•=-1, AL() = =-1, AL(2.3)=-1, AL(3.6)=-2. Видно, что оптимальное подмножество элементов состоит всего из одного Д№), определяющего перестановку модулей £з и Ее, причем суммарная длина связей сокращается на 2. Таким образом Li=i7. Размещение, полученное после первого цикла алгоритма, показано на рис. 1.15, б.