Успешное решение задач радиолокационного наблюдения возможно лишь путем наиболее полного использования различий как во временной {спектральной), так и в пространственной структуре полезных и мешающих сигналов, воздействующих На приемную антенну РЛС. В этом отношении фазируемые антенные решетки (ФАР) Обладают рядом преимуществ по сравнению с непрерывными апертурами, так как в ФАР имеется принципиальная возможность управления амплитудно-фазовым распределением (АФР) токов в отдельных излучателях антенной системы Это позволяет программно или адаптивно изменять пространственную ориентацию и форму диаграммы на йравленности, формировать необходимое количество приемных лучей с требуемыми пространственными (и пространственног временными) характеристиками, оперативно (в темпе радиолокационного наблюдения) осуществлять изменение пространственно-временных характеристик приемной антенны в соответствии с меняющейся радиолокационной ситуацией

Перечисленные возможности ФАР привели р последние годы к быстрому развитию теории и техники адаптивных РЛС, или адаптивных фазируемых антенных решеток (АФАР), в которых функции антенны и приемного устройства обработки сигналов органично связаны, а процесс адаптации заключается в опти-мизацци пространственно-временной обработки (в собтветствии с некоторым критерием качества) в условиях априорной неопределенности о структуре или параметрах полезных и мешающих сигналов

Задачи синтеза оптимальных алгоритмов обработки относятся к классу задач отыскания экстремума некоторого функционала, характеризующего качество обработки При решении таких задач часто оказывается, что безусловный экстремум достигается вне области допустимых значений варьируемых величин (или вне класса допустимых функций), поэтому приходится

довольствоваться приближенным условно экстремальным ре-щением, которое определяется проекцией безусловного на допустимую область Эти соображения имеют прямое отношение К оптимизации пространственной обработки, так как управление АФР На раскрыве антенной решетки (АР) тесно связана с задачами синтеза антенн с заданными свойствами направленности, поэтому полученные, решения должны принадлежать к классу реализуемых диаграмм направленности В этой связи кратко рассмотрим элементы общей теории АР и математические модели взаимодействия сш налов и помех в ФАР

§ 1.1 ОПИСАНИЕ ПОЛЯ В РАСКРЫВЕ ПЛОСКОЙ АР

Рассмотрим скалярное поле (без учета поляризации) в двумерном раскрыве, расположенном в плоскости х, у (рис 11), создаваемое точечным источником в точке q дальней зоны с

излучения, находящимся

координатами Xq, yq, Zf

Пусть временная структура излучаемого сигнала определяется выражением

S(0=V2P:Re(;7a(OX Хехр [(/ <йо + W {t))]),

(1 1)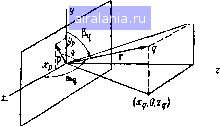

Рие 1 1 К определению поля* в произвольной точке раскрыва антенны

И фазовой модуляции, причем

1где Ps- средняя мощность излучаемого сигнала, «о - рабочая частота Vait), Т(0-законы амплитудной Ua{t) нормирован так, что

Гм- период модуляции

Для определения поля в произвольной точке раскрыва р{хту, УрУ найдем евклидово расстояние между точками ряд

I г - р I = [(г - р)~ (г -,р)] = [I г г - 2 (р. г) + I р \Т, (1 2)

где г и р - радиусы-векторы точки наблюдения q (Хд, у, Zq) и произвольной точки раскрыва, (р, г) Л р"" г--скалярное произведение векторов риг, \тильда означает транспонирований (и сопряжение для унитарных пространств)

В дальней зоне всегда выполняется условие гр, что соответствзет предположению о плоском фронте волны, поэтому, вычисляя приближенно квадратный корень, найдем

;(r p)~{r-p)]«r-rrRe(p, r) = rI-lpcosv, (1 3) где V - угол между векторами риг