

|
|
Главная -> Теория антенных решеток 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 строится на основе более простых двучленных соотношений [30] Ускорение процесса последовательных приближений реализуется в модификации алгоритма путем проектирования" решения на М-мерное подпространство в соответствии с (2 82) При этом г-е приближение вычисляется по формуле WM(i) = WM(f-1) + а,, = ШлИ0)+Е Щ,. (2 85) где Wm(0) - начальное приближение (обычно Wm(0) = Vqm), - вектор направления спуска на t-u шаге процедуры, а» - постоянная, определяющая величину шага в направлении Теоретически в методе сопряженных градиентов строится две системы векторов - взаимно ортогональная система векторов-невязок (градиентов) Го, Гь t , Гм-1, где г, = VoM - -SmWm(0 , - ортогональная в метрике Вм (Л-ортогональная) система базисных векторов i, , 9м, которая получается процессом Л-ортогонализации векторов-невязок Таким образом, в отличие от метода Л-минимальных итераций исходная система векторов, подвергающихся Л-ортогонализации, не задается заранее, а формируется последовательно на каждом шаге процедуры Практический алгоритм метода сопряженных градиентов описывается рекуррентными двучленными соотношениями Wm(0) = VoM, Го = Vom - BaiVoM, 1 = Го, (2 86) +1 = г. + р,„ р, = I г, iVl г, -, 1 = ~гТВиЛ&7Вм&-) Подставляя коэффициенты а, в (2 85) и полагая l = M, получим WM(M)==WM(0) + f Jj Го==Шм(0) + /=1 / м/ - Z тт « Wm(0) -f 2 -177v-" Vo, (2 87) + f VoM - BmWm (0)1 - / = 1 где Cj = I- матрица проектирования на одномерное подпространство, коллинеарное вектору - отношение помеха/шум, имеюшее тот же смысл, что и в (2 84), кроме того, учтено, что С,РжУо - C,Vo Таким образой, разложение /С-мерного пространства представления сигналов в прямую сумму подпространств при выполнении условия К>М применение методов сопряженных направлений для формирования проекции решения в ЛГ-мерном подпространстве позволяет реализовать итерационную вычислительную процедуру, сходящуюся за М шагов к оптимальному решению Покажем теперь, что проекторы Рк-м = 1к - Рм и Рм, осуществляющие разложение пространства, могут быть вычислены по рекуррентным соотношениям за М шагов Пусть Vi, V2, .., Vm - линейно независимые векторы размерности (itxl), принадлежащие М-мерному подпространству Тогда имеем соотношения Рк-о = 1к, Рк-. = Рк-о- (288) Р V VP рк-т = рк-m+i--тртт---, m=l, 2, ,м Отсюда следует рекуррентная процедура вычисления весового вектора, реализующего полное подавление мешающих сигналов (2 59) Wi (0) = V„, Wi (т) wnm - 1) - Z;+"У" - 1), (2 89) Wi() = Pc-MVo Соотношения (2 85), (2 86), (2 88) и (2 89) в совокупности дают алгоритм формирования оптимального по критерию МСШ весового вектора пространственной обработки Практически вычислительный процесс протекает в таком порядке 1) по процедурам (2 88) и (2 89) за М шагов вычисляются проекторы Рк-м, Рм и вектор vjl, 2) по процедурам (2 85) и (2 86) вычисляется вектор Wm за последующие М шагов Приведенные соотношения удобны для расчетов асимптотических характеристик эффективности обработки в задачах обнаружения Кроме того, они дают основу для построения адаптивных алгоритмов в условиях, когда ковариационная матрица формируется по обучающей выборке мешающих сигналов Xi, Х2, , \п (в отсутствие полезного сигнала) Практические адаптивные алгоритмы, как это следует из приведенного анализа, можно построить на комбинировании прямых методов псевдообращения выборочной матрицы для построения вектора Wb и итерационных методов типа сопряженных направлений для ч/ч ом 1 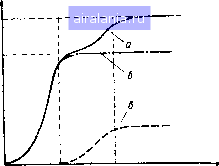 п 2Н Рис 21 Зависимость энергетического отношении сигнал/шум от объема выборки а-оптимальный ведтор B-Wj-l-Wjy., б - проек цня W (Полное подавление мешающих сигиа лов), в - проекция Wв ЛГ-мерном подпро странстве формирования вектора Из (2 87) и (2 89) следует, что весовой вектор, оптимальный по критерию МСШ, может быть представлеа в виде W = Wi + WM = (2 90) Анализ полученного разложения позволяет сделать ряд выводов При большой интенсивности мешающих сигналов (q, э>1) оптимальная обработка совпадает q условно-оптимальной по критерию МСШ при полном подавлении мешающих сигналов, т е определяется вектором Wi, Для адаптивного формирования вектора W, требуется порядка М статистически независимых выборочных векторов X, Этот вывод совпадает с результатами, полученными Ю И Абрамовичем [16], который впервые показал возможность существенного сокращения объема обучающей выборки для настройки АР. Для произвольной интенсивности мешающих сигналов при условии К>М следует формировать обе проекции весового вектора Требуемый объем обучающей выборки при этом возрастает до величины порядка -2Af- „ Эти результаты, по-видимому, близки к предельному быстродействию адаптивных алгоритмов и намного превышают скорость сходимости простых градиентных процедур. Качественный характер изменения отношения сигнал/шум на выходе канала обнаружения от объема обучающей выборки п представлен на рис 2 1 Практическая реализация устойчивых алгоритмов в большой степени, зависит от правильности определения размерности 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 0.0125 |