чтобы боковые -лепестки спектра сглаженного ряда не превышали заданный уровень

Метод весового окна хорошо сочетается с различными диа-граммообразующими схемами, которые находят широкое применение в многолучевых АР Рассмотрим его использование на

-/3,5 Э5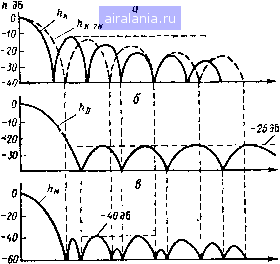

Рис- 2 3 Множители равномерно возбужденной АР (а), дольф чебышевской подрешетки (б) и модифицированной АР (в)

примере эквидистантной АР с диаграммообразующей схемой, формирующей веер диаграмм вида

sm -К (а- a) hj{a) = --, i = l,2, (2 122)

(а -аЛ

где а, = 2щ1К - координата максимума /-го луча

Набор диаграмм h, (а) образует ортогональную систему функций на интервале видимых углов, однако каждая парциальная диаграмма имеет уровень боковых лепестков 13,5 дБ Уменьшение уровня боковых лепестков достигается путем образования взвешенных сумм вида

% + N

gk{a)= Z Р-А(а), /г = 1, 2, . ,/С. / = 1, 2, . . ,/С,

(2 123)

где fe(a) - парциальная диаграмма, имеющая максимум в направлении ак и уменьшенный уровень боковых лепестков.

рлг-/ - весовые коэффициенты окна, «ширина» которого в базисе {h, (а)} равна 2Л+ 1

Весовые коэффициенты в (2 123) подчинены условию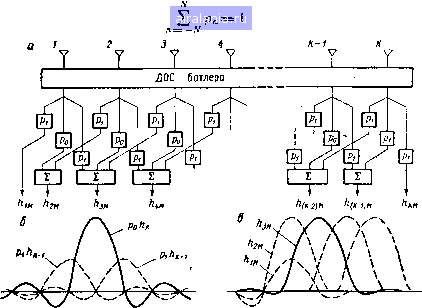

Рис 2 4 Реализация свертки окна Хемминга с диаграммами вида smc [/ (а), принцип уменьшения боковых лепестков (б), модифицированные диаграммы (в)

Из анализа соотношения (2 123) легко установить связь весового окна с методом факторизации диаграммы направленности Если учесть, что ортогональной системе {hj (а)} соответствует ортогональный базис векторов парциальных АФР, то весовой вектор, соответствующий преобразованной диаграмме gk{a), представляет собой результат линейной свертки вектора исходного АФР с весовой функцией окна

На рис, 2 4 иллюстрируется реализация весового окна с использованием ДОС Батлера

Широко известными являются симметричные трехточечные {N=1) и пятиточечные {N - 2) окна, для которых в соответствии с (2 123) получим выражения преобразованной диаграммы

gi (а) = -.(«) -Ц- 4- /г, (а) Р + Л. -V. («) ,

gf (а) , (а) + /г, , (а) + /г, (а) р, +

-iirAft + ,(a)-4?- + /tft4.2(a)-

(2 124)

Компоненты весового вектора, соответствующего g (а) с точностью до фазового сдвига, управляющего положением максимума, определяются выраже-

ниями

Wt = p + ilp)cos (2i-l)X

(для четного К),

wt=p + il-p) cos 1)Х Х(2я/)](для нечетного К)

(2 125)

Эти соотношения являются дискретным аналогом АФР типа «косинус на пьедестале», которое используется в апер-турных антеннах дЛя снижения уровня боковых лепестков и имеет вид

W (х)р+ (1р)cos (nx/L),

где х, L - координата и длина непрерывного раскрыва

В цифровом сглаживании временных рядов в зависимости от величины параметров р или ро, 1,2 реализуются окна Хемминга или Тьюки-Хана и пятиточечное окно Блэкмана

КНД решетки с MHOnte-лем определяется фор-

мулой [23]

G =

1+2[(1-р)/р]2

На рис 2 5 приведены множители решеток, соответствующие различным весовым окнам Анализ параметров диаграмм направленности показывает, что сравнительно простая весовая обработка парциальных лучей позволяет получить характеристики направленности, близкие к оптимальным Так, например, для окна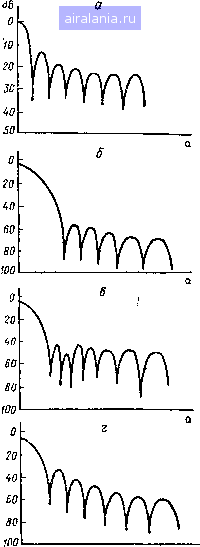

Рис 2 5 Иллюстрация подавления боковых лепестков методом весового окна

а - равномерно возбужденная АР б - окно Блэкмана в - окно Хемминга г - окно Тьюки Хана