После замены переменной в (5 32) получим распределение

Интегрируя (5 33) по найдем

1 . (2/г - 1) (2/г-3)11 t

1-2 -г (2/г-2)11 [\-tY + h

(2/г-1) {2n-2k-\)

feo an-l) (/г-2) .(/г-fe-l)

Х(1-/Г(+). (5 34)

где / = PoCos(2aop -1))

Полученное распределение характеризует свойства сглаженной по п выборкам разности фаз двух произвольно коррелированных процессов и является обобщением результатов, приведенных в [57], для случая п=\ Из анализа (534) следует, что число членов ряда зависит от объема обрабатываемой выборки и для небольших значений п не вызывает затруднений в расчетах Распределение яр симметрично относительно моды, равной 2аор, и является периодической функцией, поэтому его моменты следует определять как моменты угловой величины, распределенной на круге [50]

Характер функции И(ф) иллюстрируется на рис 5 1 для различных значений п и моды (ось абсцисс нормирована к я/2)

Наряду с распределением оценки из (5 32) и (5 33) могут быть получены распределения модуля выборочного комплексного коэффициента корреляции Го и связанной с ним величины

г 1 In ! + ">

2 1 - Го Интегрируя (5 32) по яр, получим

0)

2п~1

V- V (4«-2fe-3)M(2fe-l)4 / l-roRoY о.

X Z.„-(2/г-й-1)1Ы-\\+roRo ) "

(4п - 2fe - 3) II (2fe -1)4 / 1 - roRo fe

где P2n-i(x) - полином Лежандра [51] 164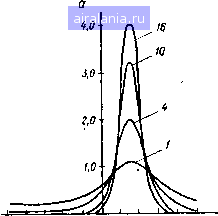

-0,8 -0,t, 0 Oft 0,8 2a,

Рис 5 1 Плотность распределения оценки ортогональной регрессии для различных средних значений

а -Дс=0,5, 2адр=0,3, 4 10, 16, б -;?о-0 5 2аор=0 8, «=1, 4, 10, 16

Аналогично, интегрируя по -ф выражение (5 33), найдем

1Г/(;Ч (2n-l)shg

2n-l

(4n-2fe-3)M (2Jfe-l)M *-o (2n-fe-l)ife

И-£) f (5 36)

. = ArthP„ = -i-lnl±f-.

Приведенные распределения могут быть использованы для определения точностных характеристик измерителей при числовых расчетах, однако желательно получить явные выражения для моментов распределения

§ 5 4. СВЯЗЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ОЦЕНОК ОРТОГОНАЛЬНОЙ РЕГРЕССИИ С РАСПРЕДЕЛЕНИЕМ МИЗЕСА ТОЧНЫЕ ФОРМУЛЫ МОМЕНТОВ

Функция плотности вероятности ОР-оценки (5 34) является периодической с интервалом периодичности [О, 2л], поэтому моменты распределения однозначно связаны с тригонометрическими моментами Эта связь устанавливается из свойств характеристической функции (X Ф ) периодических распределений

По определению X Ф случайной величины яр равна (см (5 Ш))

2я 2я(А+1)

е(м)= 5 W(ai3) ехр(у15и) dap = \ (яр) ехр (/яри) йы,

о 2яй

где k - любое целое число

Вследствие периодичности функции и(яр) X Ф оказывается определенной лишь при целочисленных значениях и = рп представляется в виде последовательности тригонометрических моментов

2я(* + 1) 2я

Тр == 5 W ехр (гряр) d = \w (яр) cos (ряр)яр + / X

Ink о

xS и7(яр)51п(ряр)(яр = Рр+уур, р = 0, ±1, ±2, (5 37)

Если тригонометрический момент порядка р вычисляется относительно некоторого направления, заданного углом щ = = vo(mod2n), то вместо (5 37) получим

Тр (vo) = S (яр) ехр [ 7 (яр - v„)] яр = (v„) + уур (vo) (5.38)