где Мг] - элементы ковариационной матрицы измерительных каналов, определяемые в отсутствие полезного сигнала

Представляет интерес произвести сравнение флюктуационных характеристик алгоритмов формирования ЛР- и ОР-оценок в одинаковых условиях, т е когда декорреляция сигналов в измерительных каналах осуществляется одним и тем же способом (например, методом Грама-Шмидта), а для измерения угловой координаты используются приближенное (4 31) или точное (4 66) решения уравнения правдоподобия

Подставляя значения параметров из (5 64) в (5 63) и полагая

р (ыо) det М/Ми, g-д (Mo)/g2 («о) = М,2/Мп, найдем Ф X алгоритма (4 31)

( = M»o)il+.) 4г (1 + + 74)

где 82 - угловая координата, отсчитываемая по пеленгациониой характеристике (4 32)

Анализ выражения (5 74) показывает квадратичную зависимость Ф Хдр от углового рассогласования относительно опорного направления «о и наличие независящей от объема выборки составляющей полной- ошибки, которая возникает из-за смещения оценки

Определим теперь флюктуационную характеристику алгоритма (4 66), реализующего ОР-оценку Для этого подставим параметры из (5 73) в (5 72)

Ф = Т(М" ~t f+ + о + з)-]. (5 75)

где бз - угловая координата, отсчитываемая по пеленгациониой характеристике (4 67)

Из сравнения выражений (5 75) и (5 74) следует, что полная ошибка измерений уменьшается с увеличением объема выборки и в отличие от (5 74) Ф Хор обратно пропорциональна квадрату углового рассогласования Это качество оказывается весьма важным для прямоотсчетных измерителей, так как позволяет существенно расширить сектор пеленгации без ухудшения точности измерений

На рис 5 2 и 5 3 приведены пеленгационные и флюктуаци-оиные характеристики для ситуации, когда источники мешающих сигналов расположены вне основных лучей измерительных диаграмм

Рис 5 4 иллюстрирует ситуацию, когда один из источников мешающих сигналов воздействует по основным лучам суммарной и разностной диаграмм Из сравнения алгоритмов формиро-

вания ЛР- и ОР-оценок следует, что точные решения уравнения правдоподобия в совокупности с методами стабилизации или коррекции П X позволяют обеспечить более высокую точность измерения угловых координат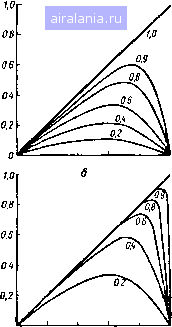

в 02 ОМ 06 08 10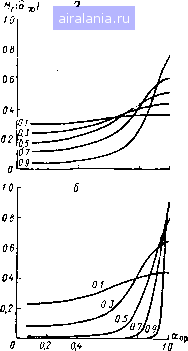

0,S 08

Рис 5 2 Пеленгационные характеристики алгоритма ортогональной регрессии

а - п-\ «0=0 2 04 06 08 09 б - п=10 i?o-0 2 04 06 08 09

Рис 5 3 флюктуационные характеристики алгоритма ортогональной регрессии

а - п=1 Ло=0 1 0 3, 05 07 09 б-п=10 Ло-О I 03 0 5, 07 09

Важно отметить, что точностные характеристики алгоритмов формирования ЛР- и ОР-оценок могут быть выражены через обобщенные параметры, а именно -через элементы матрицы ковариаций напряжений в измерительных каналах при отсутствии полезного сигнала (Mt,) и при наличии (а, а,

/10"2ад) Это позволяет построить обобщенные характеристики

12 Зааз № 199

S(a.) эб

-10 -OJS -0.В -04 -О? О 02 0« 05 Ов 10

Рис 5 4 Пеленгационные (а) и флюктуационные (б) характеристики алгоритмов вычисления ОР- и ЛР-оценок

/ - алгоритм (4 51) без мешающих сигна

лов 2, 5 -алгоритмы (4 31) и (4 51) Полезный сигнал -л=], а = Р/Рщ=20 дБ, мешающий сигнал - а.=-О 67, a=PilP = =50 дБ

измерительного тракта для типовых задач радиолокационного наблюдения

Возможность разделения задач адаптации АР и измерения угловых координат расширяет класс приемлемых алгоритмов адаптации, а рассмотренные методы стабилизации П X успешно сочетаются с произвольными алгоритмами настройки АР при некоторых ограничениях

В заключение отметим, что приведенные в главе соотношения, характеризующие точность измерений,получены в предположении отсутствия ошибок идентификации крутизны и смещения нуля П X, а также ошибок амплитудно-фазового распределения возбуждения элементов АР Учет ошибок может быть осуществлен добавлением - во флюктуационные характеристики соответствующих параметров, однако рассмотрение этих вопросов выходит за рамки данной книги