векторами настройки в уравнении дисперсии, шесть из них входят и в уравнение оценки

Для измерителя, имеющего приемную антенну с фиксированной настройкой по поляризации, уравнение оценки находится

при подстановке df/da = (5F/dp = О в (7 30) При этом измеритель содержит только один пространственный фильтр, максимизирующий отношение сигнал/шум

Как уже было отмечено, различные упрощения алгоритма работы измерителя ведут к ухудшению его оптимальности

§ 73 МОДЕЛИРОВАНИЕ МНОГОКАНАЛЬНОГО ИЗМЕРИТЕЛЯ УГЛОВЫХ КООРДИНАТ

Для проверки работы синтезированного измерителя было проведено математическое моделирование его подоптимального алгоритма Эта проверка проводилась для измерителя одной угловой координаты объекта при внешних неизотропных по пространству белых шумах для флюктуирующего и нефлюктуирующего принимаемого от сопровождаемого объекта сигнала при фиксированной поляризационной настройке антенн приемных каналов Рассматривался измеритель, выделяющий сигнал ошибки по угловой координате только из диаграмм направленности приемных антенн- Приемные каналы, число которых во всех испытаниях /С = 3, имели диаграммы направленности с совпадающими фазовыми центрами и пересекались по уровню 0,7

Для -формирования этих диаграмм направленности использовалась эквидистантная линейная ФАР с ненаправленными элементами, число которых было равно 10 Диаграмма направленности передающей антенны формировалась на той же ФАР

и управлялась оценкой угловой координаты а таким образом,

чтобы ее максимум был направлен на а При этом ее коэффициент передачи в направлении истинного положения объекта

определялся как fn(c6 -а) В результате такого /управления энергия сигнала, облучающего объект, зависит от ошибки филь-

трации Аа = а - а и имеет максимальное значение по сравнению с другими видами управления диаграммой направленности передающей антенны

В качестве зондирующего сигнала моделировался фазомани-пулнрованный сигнал, кодированный 7-элеме нтным кодом Бар-кера

Изменение угловой координаты моделировалось марковским , процессом третьего порядка и нормировалось к ширине диаграммы направленности по уровню половинной мощности аот так, чтобы l.Soojj

в результате моделирования были получены компоненты вектора состояния х(/), оценочные значения компонент вектора

состояния x{t) и оценочное значение дисперсионной матрицы

На рис 7 2 приведены результаты моделирования измерителя для отношения сигнал/шум в приемном канале до согла-

а(к)/осо?Л(Ю/(о?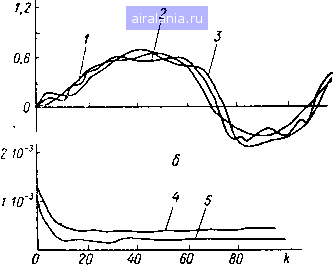

Рис 7 2 Процесс изменения угловой координаты (i), его оценки (2, 3) и дисперсии ошибок фильтрации {4, 5) для отношении сигнал/шум 5 и 10 дБ (а), (б)

сованного фильтра сжатия cni~5 и 10 дБ В результате моделирования были получены следующие значения дисперсий оценки угловой координаты рассматриваемого измерителя при

= О дБ, Уауст = 0,44 10", а = 5 дБ, Vajc. = 0,2 I0r\ а2 = ЮдБ, Гсуст = 0,12. 10-3

На рис 7 3, а-в приведены результаты моделирования измерителей угловой координаты сопровождаемою объекта при флюктуирующем сигнале Временной код излучаемого сигнала на этих рисунках тот же - 7-элементный код Баркера

Квадратурные составляющие сигнала моделировались марковскими процессами первого порядка, дисперсия каждого из которых была единичной

При наличии источников шума с угловым положением аш/ао,7 = 0,7 и а\ = 25 дБ дисперсия оценки для всех измери-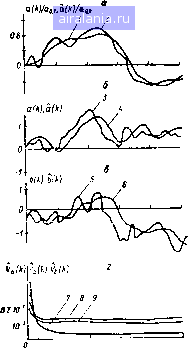

/ ?

го 40 so 80 юо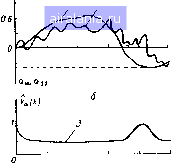

го w 60 во 100

Рис 7 3 Процесс изменения угловой координаты 1 и его оценка 2 (а), процесс изменения косинусной квадратурной составляющей сигнала 3 и его оценка 4 (б), процесс изменения синусной квадратурной составляющей сигнала 5 и его оценка 6 (в), дисперсии ощи-бок фильтрации угловой координаты 7, квадратурных составляющих сигнала 8, 9 (г)

Рис 7 4 Процесс изменения угло-вой координаты 1 и его оценка 2 (а), дисперсии ошибок фильтрации 3 (б>

телей увеличивалась Особенно это было заметно при приближении истинного значения угловой координаты сопровождаем мого объекта к угловому положению источника шума (рис 7 4, а, в) При а\ш~ - районе углового положения источника шума дисперсия оценки возрастает