Величины и направления векторов электрического и магнитного полей в различных точках по длине линии, соответствующие какому-либо фиксированному моменту времени, показаны на рис. 4. Это изображение представляет собой как бы «моментальную фотографию» поля. Если эту «неподвижную» картину перемещать вправо со скоростью распространения волны, то полученная «движущаяся» картина будет иллюстрировать процесс распространения электромагнитной волны вдоль линии. Проследим последовательные фазы этого процесса.

Допустим, что в некоторый момент времени t\ электрическое и магнитное поля распределены вдоль линии, как показано на рис. 4,а. Период колебания Г, т. е. время, в течение которого синусоидальное напряжение, приложенное к линии, проходит полный цикл изменения, связан с частотой / синусоидального напряжения следующей зависимостью:

Если с момента времени t] прошло время, равное четверти периода, то картина поля окажется сдвинутой вправо и приобретет вид, изображенный на рис. 4,6.

На рис. 4,8-д показаны соответственно картины поля вдоль линии через промежутки времени, равные половине, трем четвертям и полному периоду колебаний.

В момент времени, отличающийся от начального момента на полный период Т, картина поля имеет точно такой же вид, как и в момент времени t\- Таким образом, картина распределения векторов электрического и магнитного полей вдоль линии периодически повторяется через промежутки времени, равные целому числу периодов колебаний.

Рис. 4 не только иллюстрирует процесс движения электромагнитной волны вдоль линии, но и позволяет проследить во времени характер изменения электромагнитного поля в любом поперечном сечении линии. В качестве примера рассмотрим поле в поперечном сечении коаксиальной линии, расположенном на расстоянии / от условно выбранного начала линии- В момент времени ti векторы поля в этом сечении достигают максимального (амплитудного) значения и имеют направления, которые будем условно считать положительными.

В течение первой четверти периода колебаний (начиная с момента времени /j) векторы электрического и маг

нитного полей уменьшаются по величине, сохраняя свое направление. Ровно через четверть периода оба вектора становятся равными нулю. В течение следующей четверти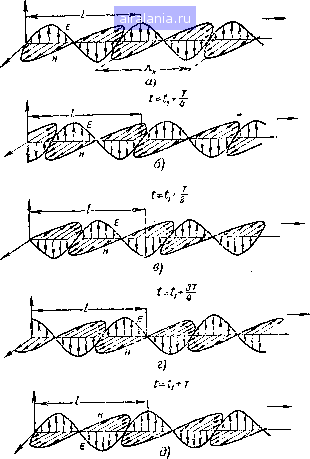

Рис. 4. Электрическое и магнит.чое поля вдоль линии передачи.

периода оба вектора увеличиваются, но имеют противоположное направление. Ровно через половину периода с момента времени ti векторы снова становятся максимальными. В течение второго полупериода колебаний векторы электрического и магнитного полей сначала уменьшаются,

2-1523 3

затем становятся равными нулю и к концу периода снова достигают максимального положительного значения.

Таким образом, через промежутки времени, равные периоду колебаний, характер электромагнитного поля как вдоль линии, так и в любом ее поперечном сечении повторяется.

Электромагнитная волна распространяется в коаксиальной линии со скоростью, которая определяется по формуле

где с - скорость света в воздухе, равная 300 000 KMJceK; S - относительная диэлектрическая проницаемость изоляции линии.

За время, равное одному периоду колебаний, волна перемещается на расстояние, равное произведению скорости распространения волны v на период колебаний Т. Это расстояние называется длиной волны в кабеле (см. рис. 4):

Длина волны в кабеле связана с длиной волны в воздухе соотношением

Например, диэлектрическая проницаемость е полиэтилена, применяемого обычно в качестве изоляции в высокочастотных коаксиальных кабелях, равна 2,3. Поэтому длина волны в кабелях со сплошной полиэтиленовой изоляцией короче длины волны в воздухе в f2,3=1,52 раза. Это явление, которое нужно учитывать в ряде практических случаев, называется укорочением длины волны в кабеле, а величина l/le -коэффициентом укорочения.

2. ПАРАМЕТРЫ КОАКСИАЛЬНЫХ КАБЕЛЕЙ

Основными параметрами кабеля являются волновое сопротивление Z, постоянная затухания р и погонная емкость С(,.

Волновое сопротивление равно отношению напряженности электрического поля в любой точке поперечного сечения линии к напряженности магнитного поля в этой 10

же точке в случае, когда электромагнитная волна распространяется вдоль линии в одном направлении, не испытывая отражения (бегущая волна).

Напряжение между проводами линии пропорционально напряженности электрического поля Е, а ток, текущий в линии, пропорционален напряженности магнитного поля Я. Следовательно, волновое сопротивление можно опреде-лить как отношение напряжения к току в режиме бегущей волны в линии. Волновое сопротивление линип с потерями не является чисто активным, а имеет и реактивную состав-ляюш,ую. Обычно затухание в линиях невелико и волновое сопротивление на практике можно считать чисто активным.

Если линию на конце нагрузить на активное сопротивление -R, численно равное волновому сопротивлению (i?=Z), то вся энергия, доходящая до конца линии, будет поглощаться в этом сопротивлении и в линии установится режим бегущей волны.

Волновое сопротивление линии определяется только формой, размерами и взаимным расположением проводников в поперечном сечении линии.

Волновое сопротивление линии связано с погонной индуктивностью Lo и погонной емкостью Со следующим соотношением:

Для коаксиального кабеля L„ и С„ определяются через геометрические размеры его поперечного сечения по следующим формулам:

L„ = 0,46 Ig J = 0,2 In mkzhIm;

41.5 Igj-

e-IO-3

181n

мкф1м.

Волновое же сопротивление коаксиального кабеля определяется геометрическими размерами его поперечного сечения по формуле

138 . D 60 , D

где D-внутренний диаметр экрана; d - диаметр центрального провода; е-диэлектрическая проницаемость изоляции.

% Zg.oM SO T--T ZiD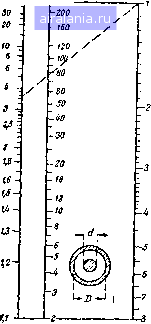

Рис. 5, Номограмма для определения волнового сопротивления коаксиальных кабелей, 2д -волновое сопротивление; D - внутренний диамето экрана: d - наружный диаметр

центрального проводника; £ -диэлектрическая проницаемость изоляции.

Рис. 6. График для определения волнового сопротивления линии с проводом круглого сечения в трубе квадратного поперечного сечения.

В некоторых устройствах иногда применяются несимметричные экранированные линии с. квадратными или иными по форме поперечными сечениями. Волновые сопротивления несимметричных экранированных линий, отличающихся по форме поперечного сечения от коаксиальных, можно определить по кривым, приведенным на рис. 6 и 7.

Постоянная затухания (5 характеризует уменьшение мощности в линии, происходящее по мере распространения

0,2 Ofi 0,5 0,8 >0

Рис. 7. График для определения волнового сопротивления линии с ленточным проводом в трубах круглого или квадратного поперечного . сечения.

Для определения волнового сопротивления коаксиального кабеля удобно пользоваться номограммой, приведенной на рис. 5. Для этого нужно соединить на номограмме прямой линией точки, соответствующие заданному отношению D/d и заданной величине е. Точка пересечения этой прямой со средней линией номограммы определ.яет величину волнового сопротивления. С помощью этой же номограммы можно решить и обратную задачу, т. е. при заданной величине s определить отношение D/d, необходимое для получения требуемой величины волнового сопротивления. 12

электромагнитных колебаний вдоль линии. Потери мощности вызываются рассеянием энергии на активном сопротивлении проводов и в диэлектрике линии.

Обычно в справочниках приводится постоянная затухания 3 в миллинеперах на метр (мнеп/м) или в неперах на километр (неп/км). Для того чтобы определить полное затухание в кабеле, надо постоянную затухания умножить на общую длину кабеля. Например, постоянная затухания для кабеля РК-3 на частоте /=100 Мгц равна 8 неп/км. При этом в кабеле длиной /=100 м (0,1 км) полное затухание j3/ = 0,8 неп. Затухание часто выражают также в децибелах (1 неп = 8,7 дб).

.i--15-3 )3