

|
|
Главная -> Радиочастотные линии 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 [23] 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 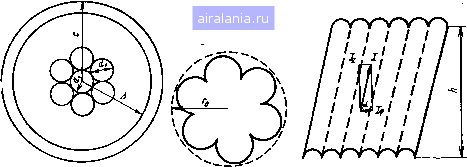 Рис. 3.13. Общий вид кон-сттрукции коаксиального кабеля с многопроводочиым виутрвияим проводником Рис. 3.14. Представление огибающей многопроволочного проводника эквивалентной окружностью Рис. 3.15. Развернутая поверхность внутреннего проводника миогрпроволочной конструкции женного расчета можно использовать различные методы. Один из них - метод «эквивалентного сечения». Согласно этому методу вначале определяют общее сечение проводника как сумму сечений отдельных проволок. Затем находят эквивалентный радиус Гэ.с или диаметр ёэ.с многопроволочного проводника. Используя значение Гэ.с или йэ.с, определяют сопротивление многопроволочного проводника по формулам, выведенным для сплошного проводника. Обозначив диаметр одной проволоки многопроволочного проводника di, а число проволок п, можно написать (3.123) Отсюда da.c = diYn или r3.c=riK«. Согласно другому способу в расчетные формулы для сплошного проводника вводят некоторый коэффициент Ки обеспечивающий совпадение расчетных данных с экспериментальными. Для семипроволочного проводника значение этого коэффициента из экспериментальных данных рекомендуется принимать равным 1,25-1,3. При этом не учитываются диаметр проволок и шаг их скрутки в многопроволочную жилу, что имеет весьма важное значение. Рассмотрим один из способов теоретического определения коэффициента Ки учитывающий диаметр и шаг скрутки многопроволочного проводника. При передаче по кабелю токов высокой частоты многопроволочный проводник можно представить в виде сплошного проводника, имеющего вид, показанный на рис. 3.14. Такое представление основано на том, что при высоких частотах вследствие явления поверхностного эффекта токи будут сосредоточены лишь иа поверхности проводчика. Проволоки проводника скручены с шагом h, и поэтому ток по такому проводнику будет распространяться по спирали. Виток такой спирали в развернутом виде показан на рис. 3.15. Наличие коаксиальной составляющей тока h и тангенциальной составляющей тика /ф обусловит соответствующие потери во внутреннем и внешнем проводниках кабеля. Общее активное сопротивление коаксиального кабеля в этом случае будет равно сум!ме сопротивлений: где Ra и Rb~ сопротивления потерь во внутреннем и внешнем проводниках за счет поперечного поля; Rax и ?ьг - дополнительные сопротивления потерь во внутреннем и внешнем проводниках за счет продольного поля. Полное сопротивление внутреннего проводника за счет поперечного поля может быть определено по формуле (3.125) Используя ур-ния (3.7) и (3.5), можно написать: (3.126) Для определения постоянной интегрирования А используем закон полного тока, согласно которому для рассматриваемого случая /sin а (3.127) где (fd/ -длина огибающей в поперечном сечении наружного пови-ва многопроволочного внутреннего проводника. При перпендикулярном сечении проволок наружного повива, свитых с шагом h, в сечении будет получаться эллипс (рис. 3.16), малая ось которого равна диаметру проволоки dl, а длина большой оси и определяется по формуле (3.123 где V - коэффициент спиральности:) v=/l"T  h» (3.129) Рис. 3.16. Сечение одной проволоки в наружном повиве многопроволочного проводника /)[-диаметр предшествующего повива (в случае семипроволоч-ного проводника Di=di). Используя известную формулу для определения длины дуги эллипса и обозначая число проволок в наружном повиве через можно написать dl = 71 tl\ dl (1 +v)-V «0. «o=-f (l+v)-]/v. (3.130) (3.131) Радиус окружности, длина которой равна длине огибающей многопроволочного проводника, будет равен (3.132) rtidi nidi -4-(i + v)-lA Полагая в ф-ле (3.126) г=го и приравнивая значения напряженностей в ф-лах (3.126) и (3.127), получаем после преобразования VrkannididoolAVrkaroY > Подставив это значение в ф-лы (3.126) и используя ур-ние (3.125), получим VikaTinididao JiiYTkaro) ЗТ I 1. Тогда (3.134) Для высоких частот (каГо>5) можно принять, что /l iVTka Го) nriididao г 2 /2(1а nkanididoo (3.135) (3.136) Для случая медного проводника („ = 4-10-7 Г/м, ра=0,0175 Om-mmVm) получим 3,35-10-* vT iiididao 5.33-10-° nidiVjdao (3.137) (3.138) В ф-лах (3.137) и (3.138) / - частота тока, Гц; d[ -диаметр одной проволоки внутреннего проводника, мм. Сопротивление внешнего проводника /?ь рассчитывается по ф-ле (3,33). Дополнительные сопротивления внутреннего проводника Raz и внешнего проводника Rbz за счет продольного поля определяются следующим образом. Применительно к продольному полю по основе основных уравнений электромагнитного поля можно написать следующее дифференциальное уравнение: дНг , I дН. + (3.139) Решение этого уравнения дает возможность найти значение напряженности магнитного поля во внутреннем и внешнем проводниках коаксиального кабеля за счет тангенциальной составляющей тока. Решением ур-ния (3.139) является выражение Я, = Ai /о [VTkr) + Bi Ко [VTkr], (3.140) где Л[ и fi, -постоянные интегрирования. При определении добавочного сопротивления Raz постоянную интегрирования Б, следует положить равной нулю, исходя из физических условий. Тогда из ур-ния (3.140) получим На.==Л,1о{ГГкаГ). (3.141) Для определения постоянной интегрирования Л, используем закон о непрерывности магнитного поля, согласно которому при г=Го НМ=Н„ (3.142) где Нь - напряженность магнитного поля в пространстве между внутренним и внешним проводниками кабеля за счет поперечной составляющей тока. Для нахождения Нь будем рассматривать внутренний проводник как бесконечный соленоид, вокруг которого концентрично расположен цилиндрический внешний проводник. Используя закон полного тока, нетрудно получить равенство Яь =/ф/Л cos а = Л. (3.143) Из этого равенства и выражений (3.141), (3.142) получаем А = -Г7-7:7РГ-- (3-144) Л/о(/1 каГо) Подставив это значение в ф-лу (3.141), получим H.z = J JoJyj ka± loiVikaro) (3.145) Значение напряженности электрического поля во внутреннем проводнике Eaz за счет тангенциальной составляющей тока можно найти по формуле Eaz = -9a-~ = --Y "P lo iVTka Го) (3.146) Зная величины Haz и Eaz, можно в соответствии с теоремой Умова - Пойнтинга легко получить следующее выражение для добавочного полного сопротивления внутреннего проводника за счет продольного магнитного поля: (3.147) Для высоких частот отношение функций Бесселя можно положить равным единице. Тогда В случае медного внутреннего проводника получим: Raz = 2,07-10- YJJhh h» 4z = 3.3-10 -5 "idiOo (3.148) (3.149) (3.150) (3.151) Yfh» • {Raz, Om/m; Laz, Г/м; dl и h, мм). Для определения дополнительного сопротивления внешнего проводника за счет продольного поля используем ур-ние (3.140), которое для рассматриваемого случая следует записать так: Hbz = /о {УТкьг) + Ко iVkbr)- (3.152) Определим постоянные интегрирования Лг и В2. Напряженность магнитного поля на внутренней поверхности внешнего проводника согласно ур-нию (3.143) будет равна А, /о [Укф) + В, Ко [УТкф] = I/h. (3.153) Напряженность магнитного поля на внешней поверхности внешнего проводника равна нулю, т. е. А /о {УТкьс) + В Ко [Vikbc) = 0. (3.154) Решив совместно два последних уравнения, получим А - KiVikbc) д f /o(/i kbc) (3.155) где М==1,{]/Ткф)Ко{Укьс)-1о{УТкус)Ко{У/гф). (3.156) Таким образом, напряженность магнитного поля во внешнем проводнике за счет тангенциальной составляющей тока будет определяться выражением (3.157) Используя это выражение, нетрудно получить формулу для напряженности электрического поля во внешнем проводнике за счет тангенциальной составляющей тока: iAYhr)Ko[Vkbc) /o(/i Кс)кЛУ V)- (3.158) Зная значения напряженностей электрического Еьх и магнитного Ньг полей и используя теорему Умова - Пойнтинга, получим в результате интегрирования следующее выражение для дополнительного полного сопротивления внешнего проводника за счет продольного поля: Kbz + 1 <в Lbz--2--дГ (3.159) Ж = /о iVhc) К, (Ki кф) - I, кф) Ко (/i kbc). (3.160) Можно показать, что для высоких частот, когда аргумент функций Бесселя больше пяти, отношение MjN\. Тогда (3.161) Rbz-V2, Lbz = V2.-. (3.162) Для случая медного проводника можно получить следующие расчетные формулы: Я„-16.5-10--. (3.163) (3.164) Теперь iBce слагаемые а ф-ле (3.124) определены, и имеется возможность написать .выражеиие для определения общего сопротивления коаксиального кабеля с многопроволочным внутренним проводником. Используя ф-лы (3.33), (3.135), (3.148) и (3.161) получаем , /2- kb 9ь (3.165) 143 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 [23] 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 0.0073 |